OPRF

在PSI中经常用到OPRF技术，现在系统学习一下。

PRF

Pseudo Random Function，伪随机函数，主要就是用来产生为伪随机数的。

伪随机数

什么伪随机数？

伪随机数是用确定性的算法计算出来自[0,1]均匀分布的随机数序列。并不真正的随机，但具有类似于随机数的统计特征，如均匀性、独立性等。C语言中的random()函数产生的随机数就是伪随机数，即假的随机数，因为每次运行生成的随机数都是一样的，所以实现生成随机数时需要种子不一样。

原理

PRF 是一个确定性的函数，记为\(F\)。

我们称\(F\)是定义在\(（k,X,Y）\)上的 PRF，其中 \(k\) 是密钥空间，\(X\) 是输入空间，\(Y\) 是输出空间。

它有两个输入，一个是密钥 \(k\)，另一个是数据块 \(x∈X\)（称作输入数据块）。它的输出\(y=F(k, x) ∈Y\) 也是一个数据块（称作输出数据块）。

对于 PRF，其安全性要求：给定一个随机产生的密钥 \(k\)，函数\(F (k,.)\)应该看上去“像”是一个定义在 \(X\) 到 \(Y\) 上的随机函数。

随机函数

给定集合\(X\)和\(Y\)，定义在\(X\)到\(Y\)上的映射\(f：X→Y\)：

首先把所有定义在\(X\)到\(Y\)上的映射集中起来，形成一个集合。这个集合里的每个元素都是一个类似\(f\)这样的映射（函数），它们的定义域都是\(X\)，值域是\(Y\)。

这个集合记为\(Funs[X,Y]\)，它就是定义在\(X\)到\(Y\)上的所有函数的集合。

很明显，这个集合里一共有\(|Y|^{|X|}\)个函数，非常大！

现在，从\(Funs[X, Y]\)随机选择一个函数。这个函数就是“随机函数”。

需要注意的是，所谓的“随机函数”强调的是这个函数是随机地被选择出来的。因此，“随机函数”这个概念和函数的输出是否是随机的没有关系。即使一个函数的输出不是随机的，但只要它被选出的时候是随机选择的，那么它就是“随机函数”。理解这一点非常重要！

实现

OPRF

Oblivious Pseudorandom Function，不经意伪随机函数。

功能

假设Alice有一些输入，Bob有一个\(key\)。OPRF允许Alice将自己的输入与Bob的\(key\)结合经过一系列运算转变成相对应的数。

在这个过程中，Alice不能知道Bob的\(key\)，Bob也不知道最后的结果\(F(key,x)\)。每一个输入\(x_i\)都可以计算出一个不同于其他输入的数，这些数就可以被看作伪随机数。

这里可以看出，里面用到了PRF，那么原理具体怎么实现呢？

原理

OPRF的实现原理有多种方法，下面介绍几种。

基于DH的OPRF

参考：Fast secure computation of set intersection.

基于DH的OPRF是计算\(F_{\alpha}(x)=H'(H(x)^{\alpha})\)，其中\(H\)是一个在\(Z_q^*\)上的hash函数，可以看作是一个喻言机。具体来说，\(G\)是一个\(q\)阶循环群，其中One-More-Gap-Diffie-Hellman(OMGDH)问题是困难的。

在Labeled PSI from Fully Homomorphic Encryption with Malicious Security 中使用的OPRF是这样的：

在Labeled PSI from Homomorphic Encryption with Reduced Computation and Communication 中使用OPRF：

那么就有疑问了：

（1）如何将item 插入到椭圆曲线上的点？

（2）如何从椭圆曲线上的点中提取\(OPRF(k,x)\)？

下面给出一种简单的方法：

该思想来自：Fast Secure Computation of Set Intersection

基于OT的OPRF

参考：隐私集合求交（PSI）-两方

基于RSA的OPRF

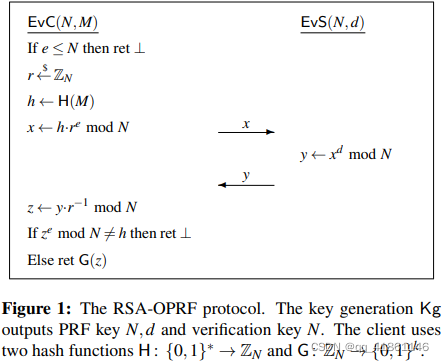
意思就是：

\(x=h.r^e\) , \(y=x^d=(h.r^e)^d\)

\(z=y.r^{-1}=(h.r^e)^d . r^{-1}=h^d.r^{ed-1}\)

\(z^e=(h^d.r^{ed-1})^e=h^{ed}.r^{e(ed-1)}\) ？？

这个没看太懂，有朋友看懂了可以解惑？

OPPRF

Oblivious Programmable Pseudo-Random Function，可编程的不经意伪随机函数。

参考：隐私集合求交（PSI）-多方

参考

1、现代密码学3.5--伪随机函数/PRF

2、【现代密码学入门】24. 伪随机函数（PRF）(1)