四边形不等式优化 dp (doing)

目录

• 1. 四边形不等式与决策单调性
• 2. 决策单调性优化 dp - (i)
• 关于符号

1. 四边形不等式与决策单调性

定义（四边形不等式）

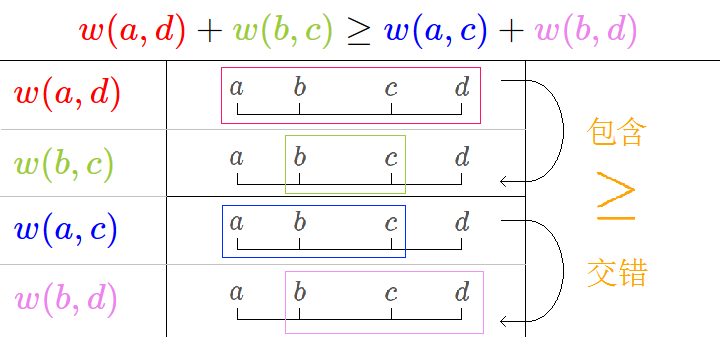
设 \(w(x,y)\) 是定义在整数集合上的二元函数，若对于任意 \(a\le b\le c\le d\)，都有

\[w(a,d)+w(b,c)\ge w(a,c)+w(b,d)
\]

则称 \(w\) 满足 四边形不等式 .

---

定义（区间包含单调性）

设 \(w(x,y)\) 是定义在整数集合上的二元函数，若对于任意 \(a\le b\le c\le d\)，都有

\[w(a,d)\ge w(b,c)
\]

则称 \(w\) 满足 区间包含单调性 .

---

定理（四边形不等式的另一种定义）

设 \(w(x,y)\) 是定义在整数集合上的二元函数，其满足四边形不等式当且仅当对于任意 \(a\le b\)，都有

\[w(a,b+1)+w(a+1,b)\ge w(a,b)+w(a+1,b+1)
\]

证明后补

---

定义（决策单调性）

设 \(w(x,y)\) 是定义在整数集合上的二元函数，

\[dp_i=\min_{0\le j<i}\{dp_j+w(j,i)\},\,p_i=\mathop{\arg\max}\limits_{0\le j<i}\{dp_j+w(j,i)\}
\]

若 \(p_i\) 在 \([1,n]\in\mathbb Z\) 上单调不减，则称 \(dp\) 具有 决策单调性

---

定理

若 \(w\) 满足四边形不等式，且

\[dp_i=\min_{0\le j<i}\{dp_j+w(j,i)\}
\]

则 \(dp\) 有决策单调性

证明后补

2. 决策单调性优化 dp - (i)

考虑维护 \(p\) 数组，根据 \(p_i\) 的单调性，可以想到 \(p_i\) 的形式大概是：

a a a a a b b b c c c c d d e
(a < b < c < d < e)

再求出一个新的 \(dp\) 时，我们可以找到一个位置，然后让后面的数全部改掉

这个用一个队列维护三元组 \((a,l,r)\) 表示 \([l,r]\) 的决策全部是 \(j\)

可以像单调队列一样排除无用决策 .

关于符号

• \(\mathop{\arg\max}\limits_x \varphi(x)\) 表示使 \(\varphi(x)\) 取到最小值的 \(x\) 的集合，\(\arg\min\) 类似 .