SpeeDO —— 并行深度学习系统

SpeeDO —— 并行深度学习系统

 

摘要: 最近，AlphaGo又带起了一波深度学习的热潮。深度学习在很多领域都大幅提高了模型的精度，使得很多以前在实验室中的技术得以运用到日常的生活之中。然而，大多数深度学习网络非常复杂，需要大量的训练样本进行训练， ...

 

 

最近，AlphaGo又带起了一波深度学习的热潮。深度学习在很多领域都大幅提高了模型的精度，使得很多以前在实验室中的技术得以运用到日常的生活之中。然而，大多数深度学习网络非常复杂，需要大量的训练样本进行训练，很多网络需要一次训练，同时额外多次的训练来调参数。时间效率上远远无法满足当前的工业需求。因此需要并行的深度学习系统提高训练速度。

 

各大公司在构建并行深度学习系统上投入了大量的精力，包括谷歌、Facebook、微软、腾讯和百度等等。为了提高算法的并行效率，这些系统大部分使用了多机多GPU的方式。所谓多机，即是大量的机器通过网络连接组成训练集群；多GPU即是集群内部的每台机器上包含多个GPU，通过数据并行（每个GPU训练部分数据）、模型并行（每个GPU训练部分网络）或者两者混合的方式提高加快训练速度。GPU浮点运行效率很高，这导致了并行系统的主要瓶颈在于I/O效率，因此这些系统使用了诸如InfiniBand和RDMA(Remote Direct Memory Access,全称远程直接数据存取，专用于解决网络传输中服务器端数据处理的延迟)等高性能技术, 而这些技术需要昂贵的硬件支持，大大增加了系统构建和维护的成本和难度，导致这些系统很难复制和普及到通用场景。

 

SpeeDO（Open DEEP learning System的逆序）是一个为通用硬件设计的并行深度学习系统。SpeeDO不需要特殊的I/O硬件，支持CPU/GPU集群，因此可以很方便地在各种云端环境上部署，如AWS、Google GCE、Microsoft Azure等等。

 

SpeeDO 采用了目前通用的参数服务器（parameter server）架构，依赖一系列基于JVM的开源库，使用Scala语言开发。

 

SpeeDO 的架构图如下图所示：

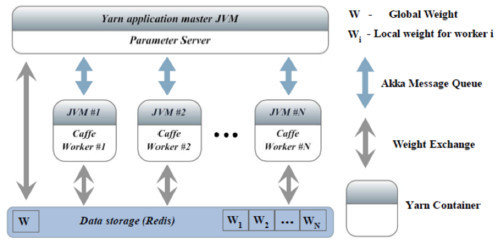流程图如下图所示:

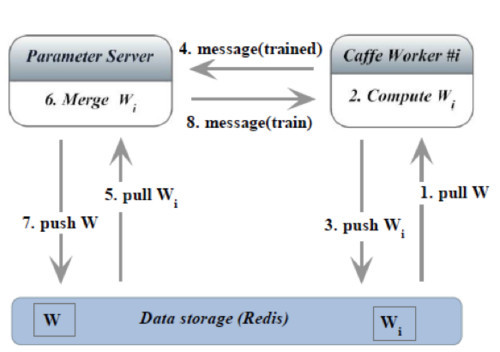SpeeDO 的主要组件及其功能如下：

 

Caffe：开源深度学习库，基于C++，支持CPU/GPU。原版不支持多GPU/多机并行。

 

Akka：JVM上的消息队列库，负责参数服务器和工作节点之间的并发消息处理。

 

Redis：基于内存的高效并行Key-Value数据库。主要用于在参数服务器和工作节点之间传递训练的模型。这些模型一般比较大（几十至上千MB不等），不适合直接通过Akka进行传输。

 

Yarn：Hadoop2的资源管理组件，实现在多台机器上一键部署参数服务器和工作节点，实时监控各节点的运行状态，处理异常。

 

SpeeDO 提供docker镜像（只支持CPU）以方便系统的快速构建和测试，获取镜像：docker pull obdg/speedo:latest，使用方法请参考：https://github.com/openbigdatagroup/speedo。

 

关于SpeeDO 的更多细节，可以参阅发表在NIPS 2015 Machine Learning Systems Workshop上的论文：http://learningsys.org/papers/LearningSys_2015_paper_13.pdf。

 

SpeeDO的代码在Github上开源：https://github.com/openbigdatagroup/speedo，并提供了详细的安装脚本和Docker文件。

 

欢迎加入本站公开兴趣群

商业智能与数据分析群

兴趣范围包括各种让数据产生价值的办法，实际应用案例分享与讨论，分析工具，ETL工具，数据仓库，数据挖掘工具，报表系统等全方位知识

QQ群：81035754

 

 http://www.oschina.net/p/speedo

http://bi.dataguru.cn/

http://chuansong.me/account/gh_5906530d307c