@topcoder - SRM611D1L3@ ElephantDrinking

目录

• @description@
• @solution@
• @accepted code@
• @details@

---

@description@

给定有一个 n*n 的平原，其中一些格子有些泉水。泉水每单位时间生产的水量有多有少。

平原周围有 4*n 头大象，如下图所示的绿色部分。大象可以将鼻子笔直伸向自己面对的方向喝泉水（假设鼻子长到可以触碰对面边缘），如下图所示红色线段。

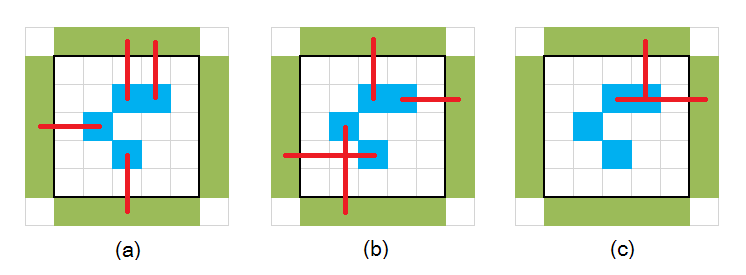
本题还有些额外限制：大象的鼻子不能相交；每个泉水最多被一个大象占领。如图 (a) 是合法的，图 (b) 都算大象的鼻子相交。

请计算大象们每单位时间最多能喝多少的水。

Class:

ElephantDrinking

Method:

maxSum

Parameters:

String[]

Returns:

int

Constraints

n 在 2 到 50 之间。通过字符串数组来描述平原，其中字符串 i 的第 j 位为一个 '0'~'9' 的数，描述平原 (i, j) 的单位时间产水量（0 则不产水）。

Examples

0）

{"00000",

"00110",

"01000",

"00100",

"00000"}

Returns: 4

1）

{"111",

"191",

"111"}

Returns: 16

@solution@

这个 dp。。。虽然不难理解。。。但是好像有点乱搞。。。

（注：以下的图片都不是我画的，是从其他地方截下来的）

首先我们令 a 表示最左面的大象的鼻子向右最远延伸到多少行，同理定义 b 表示最右，c 表示最下，d 表示最上。

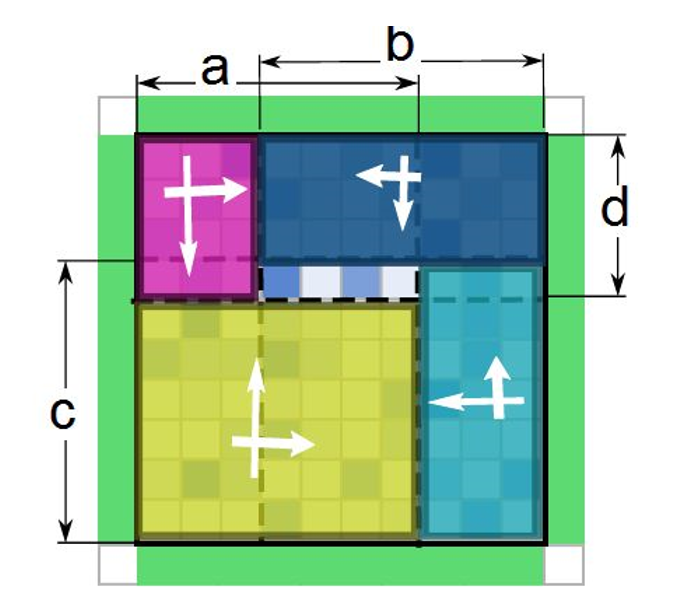
考虑如果 a <= b，实际上中间形成了一条可以供上下的大象自由伸展鼻子的区域（如下图）。

我们假设预处理出 f[i][j] 表示仅考虑左大象和上大象时，取矩阵左上部分到 (i, j) 这一区域的最优答案。同理再预处理出仅考虑左、下；仅考虑右、上；仅考虑右、下的值。

则上图中蓝、黄、青、紫区域的答案就是我们预处理出来的值。

橙色区域实际上每一列只会有两头大象，所以处理出每一列的最大值与次大值之和即可。

如果 d <= c，其实就是把上下变成了左右，一样的处理即可。

如果 a > b 且 d > c，实际上形成了像是弦图的模样（如下图）：

只需要枚举中间那个空的矩形即可，一样利用我们预处理好的信息。

当然它还可以转个方向（如下图），不过处理方法还是一样：

现在考虑怎么预处理出 f[i][j] 呢？这里仅说明左、上的情况，其他情况类似。

我们枚举最后一行的大象鼻子延伸的位置；再枚举一列，使那一列上面的大象鼻子延伸至最后一行，且那一列左边没有任何大象延伸至最后一行。枚举的那一列右边的大象没有限制，故肯定延伸至最大泉水处。

这样总时间复杂度就是 O(n^4) 的，可以很轻松地跑过。

@accepted code@

#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN = 50;
class ElephantDrinking{
	public:
	int a[MAXN + 5][MAXN + 5], n;
	int tmp[MAXN + 5], res;
	int f1[MAXN + 5][MAXN + 5];
	void get_lu() {
		for(int j=1;j<=n;j++) tmp[j] = 0;
		memset(f1, 0, sizeof f1);
		for(int i=1;i<=n;i++) {
			for(int j=1;j<=n;j++) {
				tmp[j] = max(tmp[j], a[i][j]);
				for(int k=0;k<=j;k++) {
					res = a[i][k], f1[i][j] = max(f1[i][j], res + f1[i-1][j]);
					for(int l=j;l>k;l--)
						res += tmp[l], f1[i][j] = max(f1[i][j], res + f1[i-1][l-1]);
				}
//				printf("* %d %d : %d\n", i, j, f1[i][j]);
			}
		}
	}
	int f2[MAXN + 5][MAXN + 5];
	void get_ld() {
		for(int j=1;j<=n;j++) tmp[j] = 0;
		memset(f2, 0, sizeof f2);
		for(int i=n;i>=1;i--) {
			for(int j=1;j<=n;j++) {
				tmp[j] = max(tmp[j], a[i][j]);
				for(int k=0;k<=j;k++) {
					res = a[i][k], f2[i][j] = max(f2[i][j], res + f2[i+1][j]);
					for(int l=j;l>k;l--)
						res += tmp[l], f2[i][j] = max(f2[i][j], res + f2[i+1][l-1]);
				}
//				printf(". %d %d : %d\n", i, j, f2[i][j]);
			}
		}
	}
	int f3[MAXN + 5][MAXN + 5];
	void get_ru() {
		for(int j=1;j<=n;j++) tmp[j] = 0;
		memset(f3, 0, sizeof f3);
		for(int i=1;i<=n;i++) {
			for(int j=n;j>=1;j--) {
				tmp[j] = max(tmp[j], a[i][j]);
				for(int k=n+1;k>=j;k--) {
					res = a[i][k], f3[i][j] = max(f3[i][j], res + f3[i-1][j]);
					for(int l=j;l<k;l++)
						res += tmp[l], f3[i][j] = max(f3[i][j], res + f3[i-1][l+1]);
				}
//				printf("? %d %d : %d\n", i, j, f3[i][j]);
			}
		}
	}
	int f4[MAXN + 5][MAXN + 5];
	void get_rd() {
		for(int j=1;j<=n;j++) tmp[j] = 0;
		memset(f4, 0, sizeof f4);
		for(int i=n;i>=1;i--) {
			for(int j=n;j>=1;j--) {
				tmp[j] = max(tmp[j], a[i][j]);
				for(int k=n+1;k>=j;k--) {
					res = a[i][k], f4[i][j] = max(f4[i][j], res + f4[i+1][j]);
					for(int l=j;l<k;l++)
						res += tmp[l], f4[i][j] = max(f4[i][j], res + f4[i+1][l+1]);
				}
//				printf("! %d %d : %d\n", i, j, f4[i][j]);
			}
		}
	}
	int solve1() {
		int ret = 0, res1 = 0, res2 = 0, res3 = 0, mx = 0, smx = 0;
		for(int i=0;i<=n;i++) {
			res1 = res2 = 0;
			for(int k=1;k<=n;k++)
				res1 = max(res1, a[k][i] + f1[k-1][i] + f2[k+1][i]);
			for(int j=i+1;j<=n+1;j++) {
				res3 = 0;
				for(int k=1;k<=n;k++)
					res3 = max(res3, a[k][j] + f3[k-1][j] + f4[k+1][j]);
				ret = max(ret, res1 + res2 + res3);
				if( j == n + 1 ) break;
				mx = smx = 0;
				for(int k=1;k<=n;k++) {
					if( a[k][j] > mx )
						smx = mx, mx = a[k][j];
					else if( a[k][j] > smx )
						smx = a[k][j];
				}
				res2 += (mx + smx);
			}
		}
		return ret;
	}
	int solve2() {
		int ret = 0, res1 = 0, res2 = 0, res3 = 0, mx = 0, smx = 0;
		for(int i=0;i<=n;i++) {
			res1 = res2 = 0;
			for(int k=1;k<=n;k++)
				res1 = max(res1, a[i][k] + f1[i][k-1] + f3[i][k+1]);
			for(int j=i+1;j<=n+1;j++) {
				res3 = 0;
				for(int k=1;k<=n;k++)
					res3 = max(res3, a[j][k] + f2[j][k-1] + f4[j][k+1]);
				ret = max(ret, res1 + res2 + res3);
				if( j == n + 1 ) break;
				mx = smx = 0;
				for(int k=1;k<=n;k++) {
					if( a[j][k] > mx )
						smx = mx, mx = a[j][k];
					else if( a[j][k] > smx )
						smx = a[j][k];
				}
				res2 += (mx + smx);
			}
		}
		return ret;
	}
	int solve3() {
		int ret = 0;
		for(int i=1;i<n;i++)
			for(int j=i+1;j<=n;j++)
				for(int k=1;k<n;k++)
					for(int l=k+1;l<=n;l++) {
						ret = max(ret, f1[i][l-1] + f2[i+1][k] + f3[j-1][l] + f4[j][k+1]);
						ret = max(ret, f1[j-1][k] + f2[j][l-1] + f3[i][k+1] + f4[i+1][l]);
					}
		return ret;
	}
	int maxSum(vector<string>field) {
		n = field.size();
		memset(a, 0, sizeof a);
		for(int i=0;i<n;i++)
			for(int j=0;j<n;j++)
				a[i + 1][j + 1] = field[i][j] - '0';
		get_lu(), get_ld(), get_ru(), get_rd();
		return max(max(solve1(), solve2()), solve3());
	}
}ED;

@details@

写得来，但就是想不到。。。

写的时候 Ctrl + c 与 Ctrl + v 用得很爽 2333。