CodeForce - 1189 D1. Add on a Tree (思维题）

Note that this is the first problem of the two similar problems. You can hack this problem only if you solve both problems.

You are given a tree with nn nodes. In the beginning, 00 is written on all edges. In one operation, you can choose any 22 distinct leaves uu, vvand any real number xx and add xx to values written on all edges on the simple path between uu and vv.

For example, on the picture below you can see the result of applying two operations to the graph: adding 22 on the path from 77 to 66, and then adding −0.5−0.5 on the path from 44 to 55.

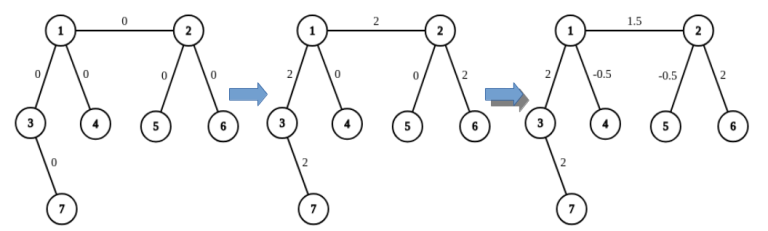
Is it true that for any configuration of real numbers written on edges, we can achieve it with a finite number of operations?

Leaf is a node of a tree of degree 11. Simple path is a path that doesn't contain any node twice.

Input

The first line contains a single integer nn (2≤n≤1052≤n≤105) — the number of nodes.

Each of the next n−1n−1 lines contains two integers uu and vv (1≤u,v≤n1≤u,v≤n, u≠vu≠v), meaning that there is an edge between nodes uu and vv. It is guaranteed that these edges form a tree.

Output

If there is a configuration of real numbers written on edges of the tree that we can't achieve by performing the operations, output "NO".

Otherwise, output "YES".

You can print each letter in any case (upper or lower).

Examples

input

Copy

2
1 2

output

Copy

YES

input

Copy

3
1 2
2 3

output

Copy

NO

 

 

 

题意：

给定一棵树，树上的边权初始为0，你可以在任意两个叶子之间的简单路径上的边上加上一个权值实数x。

问：能否在有限次数的操作内，得到边权任意组合的树

 

思路：

假设有叶子节点L1,L2,L3,并且有L1的邻居U，L1,L2和L3在以U为根节点的树的不同子树上。

现在想要U到L1边权为x，而其他边权不变。那么只需要L1-L2的路径上加上X/2，L1-L3的路径上加上X/2，L2-L3上的路径减去想x/2 即可。

显而易见要完成这个操作，U的度数要大于等于3

所以只需要判断有没有度数为2的点行了。

 

#include<iostream>
#include<algorithm>
#include<vector>
#include<stack>
#include<queue>
#include<map>
#include<set>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<ctime>

#define fuck(x) cout<<#x<<" = "<<x<<endl;
#define debug(a, x) cout<<#a<<"["<<x<<"] = "<<a[x]<<endl;
#define ls (t<<1)
#define rs ((t<<1)|1)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int maxn = ;
const int maxm = ;
const int inf = 0x3f3f3f3f;
const ll Inf = ;
const int mod = ;
const double eps = 1e-;
const double pi = acos(-);

int n;
int num[maxn];

int main() {

    scanf("%d",&n);

    for(int i=;i<n;i++){
        int x;
        scanf("%d",&x);
        num[x]++;
        scanf("%d",&x);
        num[x]++;
    }
    bool flag = true;
    for(int i=;i<maxn;i++){
        if(num[i]==){
            flag=false;
        }
    }

    if(flag){
        printf("YES\n");
    }
    else{
        printf("NO\n");
    }

    return ;
}