二叉查找树、平衡二叉树(AVL)、B+树、联合索引

1. [定义] 二叉排序树(二拆查找树)中，左子树都比节点小，右子树都比节点大，递归定义。

[性能] 二叉排序树的性能取决于二叉树的层数

• 最好的情况是 O(logn)，存在于完全二叉排序树情况下，其访问性能近似于折半查找（见下图 a）；
• 最差时候会是 O(n)，比如插入的元素是有序的，生成的二叉排序树就是一个链表，这种情况下，需要遍历全部元素才行（见下图 b）。

2. [定义] 平衡二叉树(AVL)中，符合二叉查找树的基础上，任意节点的两个子树的最大高度差为一。

需要左旋和右旋

3. [定义] B+

数据在叶子节点上，叶子节点由指针进行连接，

 

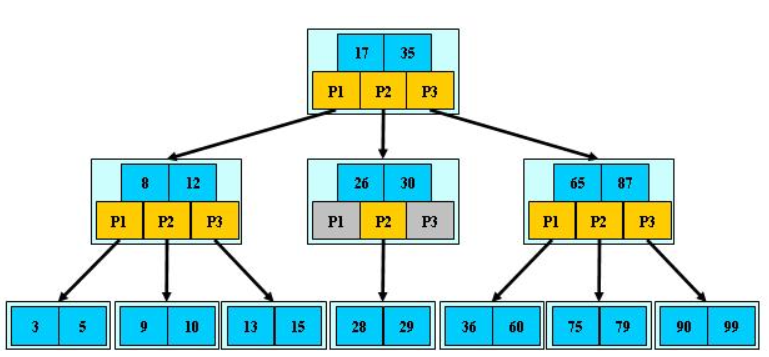
a. 二分查找的瓶颈在于树的深度，最坏的情况要查找到二叉树的最深层。

b. 由于每查找深一层，就要访问更深一层的索引文件。在多达数G的索引文件中，这将是很大的开销。所以，尽量把数据结构设计的更为‘矮胖’一点就可以减少访问的层数。

c. B+树的节点只存储索引key值，具体信息的地址存在于叶子节点的地址中。这就使以页为单位的索引中可以存放更多的节点。减少更多的I/O支出。

d. MySQL中MyIsAM和InnoDB都是采用的B+树结构。不同的是前者是非聚集索引，后者主键是聚集索引，所谓聚集索引是物理地址连续存放的索引，在取区间的时候，查找速度非常快，但同样的，插入的速度也会受到影响而降低。聚集索引的物理位置使用链表来进行存储。

4. [定义] Mysql中的联合索引也是B+树

部分内容摘自

https://blog.csdn.net/u011240877/article/details/53329023

https://www.cnblogs.com/tiancai/p/9024351.html