经典算法 Manacher算法详解

内容：

1、原始问题   =》O(N^2)

2、Manacher算法   =》O(N)

1、原始问题

Manacher算法是由题目“求字符串中长回文子串的长度”而来。比如 abcdcb 的最长回文子串为 bcdcb ，其长度为5

暴力解法：

可以遍历字符串中的每个字符，当遍历到某个字符时就比较一下其左边相邻的字符和其右边相邻的字符是否相同，

如果相同则继续比较其右边的右边和其左边的左边是否相同，如果相同则继续比较……，我们暂且称这个过程为向外“扩”。

当“扩”不动时，经过的所有字符组成的子串就是以当前遍历字符为中心的长回文子串

暴力解法的时间复杂度分析：

每次遍历都能得到一个长回文子串的长度，使用一个全局变量保存最大的那个，遍历完后就能得到此题的解。

这种方法的时间复杂度：当来到第一个字符时，只能扩其本身即1个；来到第二个字符时，多扩两 个；……；

来到字符串中间那个字符时，多扩 (n-1)/2+1 个；因此时间复杂度为 1+2+……+(n-1)/2+1 即 O(N^2) 。

但是Manacher算法却能做到 O(N)

处理回文子串长度为偶数的问题：

例如abcdcb，其中bcdcb属于一个回文子串，但如果回文子串长度为偶数呢？像 cabbac ，按照上面定义的“扩”的逻辑，

岂不是每个字符的回文半径都是0，但事实上cabbac的回文子串长度是6。因为我们上面“扩”的逻辑默认是将回文子串当做奇数

长度的串来看的，因此我们在使用 Manacher算法之前还需要将字符串处理一下，这里有个技巧，就是将字符串的首尾

和每个字符之间加上一个特殊符号，这样就能将输入的串统一转为奇数长度的串了。比如 abba 处理过后为 #a#b#b#a ，

这样的话就有 charArr[4]='#' 的回文半径为4，也即原串的大回文子串长度为4。相应代码如下：

1 public static char[] manacherString(String str){  
2     char[] source = str.toCharArray();  
3     char chs[] = new char[str.length() * 2 + 1];  
4     for (int i = 0; i < chs.length; i++) {    
5         chs[i] = i % 2 == 0 ? '#' : source[i / 2];
6     }  
7     return chs;
8 }

2、Manacher算法

Manacher算法中的相关概念：

• 回文半径：串中某个字符多能向外扩的字符个数称为该字符的回文半径。比如 abcdcb 中字符 d ，能扩一 个 c ，还能再扩一个 b ，再扩就到字符串右边界了，再算上字符本身，字符 d 的回文半径是3。
• 回文半径数组 pArr ：长度和字符串长度一样，保存串中每个字符的回文半径。比如 charArr="abcdcb" ， 其中 charArr[0]='a' 一个都扩不了，但算上其本身有 pArr[0]=1 ；而 charArr[3]='d' 多扩2个，算上 其本身有 pArr[3]=3 。
• 右回文右边界 R ：遍历过程中，“扩”这一操作扩到的右的字符的下标。比如 charArr=“abcdcb” ，当遍 历到 a 时，只能扩 a 本身，向外扩不动，所以 R=0 ；当遍历到 b 时，也只能扩 b 本身，所以更新 R=1 ； 但当遍历到 d 时，能向外扩两个字符到 charArr[5]=b ，所以 R 更新为5。
• 右回文右边界对应的回文中心 C ： C 与 R 是对应的、同时更新的。比如 abcdcb 遍历到 d 时， R=5 ， C 就是 charArr[3]='d' 的下标 3

Manacher算法实质上是利用了遍历过程中计算的pArr、R、C来为后序字符的回文半径的求解加速：

情况1  遍历到的字符下标 cur 在 R 的右边(开始时R=-1)

在这种情况下该字符的大回文半径 pArr[cur] 的求解无法加速，只能一步步向外扩来求解。这种情况实际上只能用暴力解法，无法加速

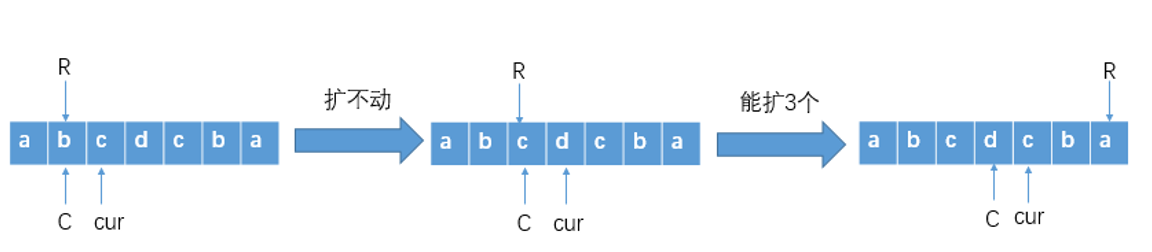
情况2  遍历到的字符下标 cur 在 R 的左边

这时 pArr[cur] 的求解过程可以利用之前遍历的字符回文半径信 息来加速。分别做 cur 、 R 关于 C 的对称点 cur' 和 L：

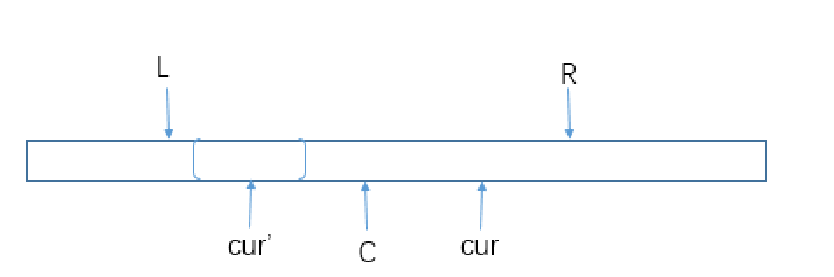
• 如果从 cur' 向外扩的大范围的左边界没有超过 L ，那么 pArr[cur] = pArr[cur']
• 如果从 cur' 向外扩的大范围的左边界超过了 L ，那么 pArr[cur] = R-cur+1
• 以 cur' 为中心向外扩的大范围的左边界正好是 L ，那么 pArr[cur]   >= R-cur+1(后面的还可能继续扩)

证明省略，综上所述， pArr[cur] 的计算有四种情况：暴力扩、等于 pArr[cur'] 、等于 R-cur+1 、从 R-cur+1 继续向外扩。

时间复杂度分析：

使用此算法求解原始问题的过程就是遍历串中的每个字符，每个字符都尝试向外扩到大并更新 R （只增不减），

每次 R增加的量就是此次能扩的字符个数，而 R 到达串尾时问题的解就能确定了，因此时间复杂度就是

每次扩操作检查的次数总和，也就是 R 的变化范围（ -1~2N ，因为处理串时向串中添加了 N+1 个 # 字符），即O(N)

完整代码：

 public class Manacher {
     // 处理字符串
     public static char[] manacherString(String str) {
         char[] source = str.toCharArray();
         char[] chs = new char[str.length() * 2 + 1];
         for (int i = 0; i < chs.length; i++) {
             chs[i] = i % 2 == 0 ? '#' : source[i / 2];
         }
         return chs;
     }

     // 核心代码
     public static int maxPalindromeLength(String str) {
         char[] charArr = manacherString(str);
         int pArr[] = new int[charArr.length];
         int R = -1, C = -1;
         int max = Integer.MIN_VALUE;
         for (int i = 0; i < charArr.length; i++) {
             // 确定加速信息
             pArr[i] = i > R ? 1 : Math.min(pArr[C * 2 - i], R - i);
             // 继续扩
             while (i + pArr[i] < charArr.length && i - pArr[i] > -1) {
                 if (charArr[i + pArr[i]] == charArr[i - pArr[i]]) {
                     pArr[i]++;
                 } else {
                     break;
                 }
             }
             // 扩完之后改变R和C
             if (R < i + pArr[i]) {
                 R = i + pArr[i] - 1;
                 C = i;
             }
             max = Math.max(max, pArr[i]);
         }
         return max - 1;
     }

     public static void main(String[] args) {
         System.out.println(maxPalindromeLength("zxabcdcbayq"));
     }
 }