[计算机网络-应用层] P2P应用

首先我们要先来区分一下下面的几种体系结构：

CS：Client/Server　　客户-服务器结构
BS：Browser/Server　 浏览器-服务器结构 
P2P：Peer to Peer　　对等结构

BS其实是CS方式的一种特例，所以也应算在CS中。 
CS：主机A如果运行客户端程序，而主机B运行服务端程序，客户A向服务端B发送请求服务，服务器B向客户A提供服务，这种情况下，就是以CS的方式进行通信。我们所指的客户和服务器都是指通信中涉及的两个应用进程，而不是具体的主机。

P2P：以对等方式进行通信，并不区分客户端和服务端，而是平等关系进行通信。在对等方式下，可以把每个相连的主机当成既是主机又是客户，可以互相下载对方的共享文件。比如迅雷下载就是典型的P2P通信方式。

BS和CS通信的实质相同，都是客户端向服务器端发送请求，服务端接收并处理。但是BS相对于CS来说更方便，对电脑配置要求更低，并且易于维护，安全性在某种意义上要好些，CS中容易被反汇编，但是CS对于那种复杂的业务处理要更容易一些。

P2P的特点：

·资源共享

·资源分布

·各结点既是资源的提供者又是资源的使用者

下面是三种特别适合用P2P设计的应用程序：

（1）文件分发 （2）对等方社区中组织并搜索信息 （3）Skype，一种相当成功的P2P因特网电话应用（暂不详细说明）

1.P2P文件分发

在P2P文件分发中，每个对等方都能够重新分发其所有的该文件的任何部分，从而协助服务器进行分发。

·P2P体系结构的自扩展性

对足够大的N（对等方的数量）：

客户机/服务器体系结构的分发时间随着对等方的数量N线性增加并且没有界。

P2P体系结构，其最小分发时间曲线与log2N曲线类似，因此最小分发时间远小于客户机/服务器体系结构的分发时间。其自扩展性很强。

·BitTorrent

BitTorrent是一种用于文件分发的流行P2P协议。

2.在P2P区域中搜索信息

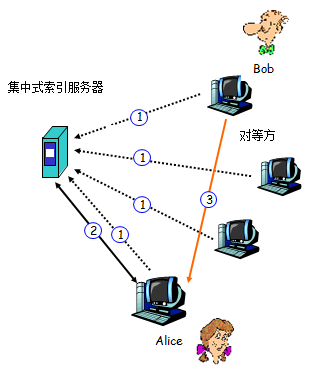
·集中式索引（初始“Napster”的设计）----P2P和CS的混合体

如下图所示：

（1）初始时，所有的对等方要将自身的IP和可共享的文件名称通知集中式索引服务器，该索引服务器从每个活动的对等方那里收集这些信息，从而建立起一个动态索引，将每个文件拷贝映射到一个IP地址集合。

（2）当Alice需要下载一些文件时会将查询内容发送给索引服务器，服务器将查询结果返回给Alice（Bob的IP地址）。

（3）Alice根据收到的信息，从Bob处下载资源。

缺点：

·单点故障。·性能瓶颈和基础设施费用。·侵犯版权。

·查询洪泛（建立在“Gnutella”协议基础上）

查询洪泛采用完全分布式方法。在查询洪泛中，索引全面地分布在对等方的区域中。每个对等方索引可供共享的文件而不索引其他文件。

其扩展性差，尤其是为了防止某个对等方发起查询，该查询就会传播到整个覆盖网络的每个其他对等方，从而产生大量流量。为解决这个问题，设计者使用了受限查询洪泛，即限制其传播的最大跳数。

·层次覆盖（由FastTrack首创，Kazza和Morpheus也实现了这种文件共享协议）

该方法结合了上述两种方法的优秀特征，与洪泛查询类似，层次覆盖设计不使用专用的服务器（或服务器场）来跟踪和索引文件。然而，与洪泛查询不同的是，在层次覆盖的设计中并非所有对等方都是平等的。

如下图所示，如果某对等方不是超级对等方，则它就是一个普通对等方，并被指派为一个超级对等方的子对等方。

超级对等方维持着一个索引，该索引包括子对等方正在共享的所有文件的标识符、有关文件的元数据和相应子对等方的IP地址，但与前面的集中式索引不同，这里的超级对等方并不是一台专用服务器，而是普通对等方。超级对等方之间可以相互建立TCP连接，从而形成一个覆盖网络。