Bellman-Ford算法——解决负权边
Dijkstra算法虽然好,但是它不能解决带有负权边(边的权值为负数)的图。
接下来学习一种无论在思想上还是在代码实现上都可以称为完美的最短路径算法:Bellman-Ford算法。
Bellman-Ford算法非常简单,核心代码四行,可以完美的解决带有负权边的图。
for(k=;k<=n-;k++) //外循环循环n-1次,n为顶点个数
for(i=;i<=m;i++)//内循环循环m次,m为边的个数,即枚举每一条边
if(dis[v[i]]>dis[u[i]]+w[i])//尝试对每一条边进行松弛,与Dijkstra算法相同
dis[v[i]]=dis[u[i]]+w[i];
在一个含有n个顶点的图中,任意两点之间的最短路径最多包含n-1条边,最短路径中不可能包含回路。
因为最短路径是一个不包含回路的简单路径,回路分为正权回路(回路权值之和为正)和负权回路(回路权值之和为负)。如果最短路径中包含正权回路,那么去掉这个回路,一定可以得到更短的路径;如果最短路径中包含负权回路,那么肯定没有最短路径,因为每多走一次负权回路就可以得到更短的路径. 因此最短路径肯定是一个不包含回路的最短路径,即最多包含n-1条边。
Bellman-Ford算法的主要思想:
首先dis数组初始化顶点u到其余各个顶点的距离为∞,dis[u] = 0。
然后每轮对输入的所有边进行松弛,更新dis数组,至多需要进行n-1次就可以求出顶点u到其余各顶点的最短路径(因为任意两点之间的最短路径最多包含n-1条边,所以只需要n-1轮就行)。
一句话概括Bellman-Ford算法就是:对所有边进行n-1次“松弛”操作。
此外,Bellman-Ford算法可以检测一个图是否有负权回路。如果已经进行了n-1轮松弛之后,仍然存在
if(dis[v[i]]>dis[u[i]]+w[i])
dis[v[i]]=dis[u[i]]+w[i];
的情况,也就是说在进行n-1轮之后,仍然可以继续成功松弛,那么这个图一定存在负权回路。
关键代码如下:
//Bellman-Ford算法核心语句
for(k=;k<=n-;k++) //外循环循环n-1次,n为顶点个数
for(i=;i<=m;i++)//内循环循环m次,m为边的个数,即枚举每一条边
if(dis[v[i]]>dis[u[i]]+w[i])//尝试对每一条边进行松弛,与Dijkstra算法相同
dis[v[i]]=dis[u[i]]+w[i];
//检测负权回路
flag=;
for(i=;i<=m;i++)
if(dis[v[i]]>dis[u[i]]+w[i])
flag=;
if(flag==)
printf("此图有负权回路");
显然,算法复杂度为O(NM),比Dijkstra算法还高,当然可以进行优化。
在实际操作中,Bellman-Ford算法经常会在没有达到n-1轮松弛前就已经计算出最短路,上面已经说过,n-1其实是最大轮回次数。
因此可以添加一个变量check用来标记数组dis在本轮松弛中是否发生了变化,若没有变化,则提前跳出循环。
完整代码如下:
#include <stdio.h> #define INF 999999
int main()
{
int i, j, n, m;
int dis[], bak[], u[], v[], w[];
int check, flag = ;
//读入n和m,n表示顶点个数,m表示边的条数
scanf_s("%d %d", &n, &m);
//读入边
for (i = ; i <= m; ++i)
{
scanf_s("%d %d %d", &u[i], &v[i], &w[i]);
}
//初始化dis数组,这里是1号顶点到其余顶点的初始路程
for (i = ; i <= n; ++i)
{
dis[i] = INF;
}
dis[] = ; // Bellman-Ford算法核心代码
for (j = ; j <= n-; ++j) //最多循环n-1轮
{
check = ;//用来标记在本轮松弛中数组dis是否发生更新
for (i = ; i <= m; ++i) // 最核心的3句Bellman-Ford算法
{
if (dis[v[i]] > dis[u[i]] + w[i])
{
dis[v[i]] = dis[u[i]] + w[i];
check = ;//数组dis发生更新,改变check的值
}
}
//松弛完毕后检测数组dis是否有更新
if (check==)
{
break; //没有更新则提前退出程序
}
} //检测负权回路
for (i = ; i <= m; ++i) // n-1次之后最短路径还会发生变化则含有负权回路
{
if (dis[v[i]] > dis[u[i]] + w[i])
{
flag = ;
}
} if (flag==)
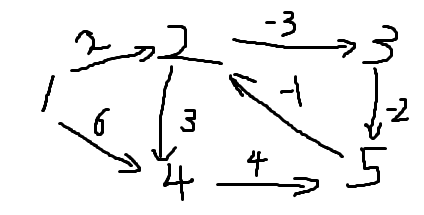
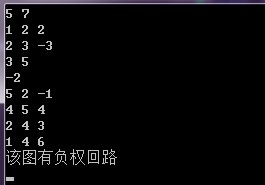
{
printf("该图有负权回路");
}
else
{
//输出最终结果
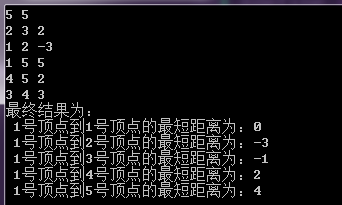
printf("最终结果为:\n");
for (i = ; i <= n; ++i)
{
printf(" 1号顶点到%d号顶点的最短距离为:%d\n", i,dis[i]);
}
}
printf("\n");
getchar();
getchar();
return ;
}
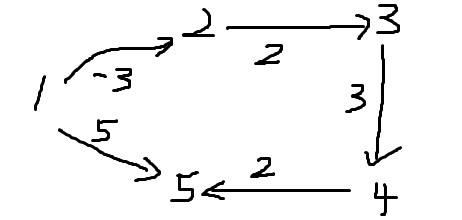
Bellman-Ford算法——解决负权边的更多相关文章
- Bellman - Ford 算法解决最短路径问题
Bellman - Ford 算法: 一:基本算法 对于单源最短路径问题,上一篇文章中介绍了 Dijkstra 算法,但是由于 Dijkstra 算法局限于解决非负权的最短路径问题,对于带负权的图就力 ...
- Bellman—Ford算法思想
---恢复内容开始--- Bellman—Ford算法能在更普遍的情况下(存在负权边)解决单源点最短路径问题.对于给定的带权(有向或无向)图G=(V,E),其源点为s,加权函数w是边集E的映射.对图G ...
- hdu1533 Going Home km算法解决最小权完美匹配
Going Home Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total ...
- Bellman-Ford(可解决负权边)--时间复杂度优化
Bellman-Ford 可解决带有负权边的最短路问题 解决负权边和Dijkstra相比是一个优点,Bellman-Ford的核心代码只有4行:: u[],v[],w[] 分别存一条边的顶点.权值,d ...
- python数据结构与算法——图的最短路径(Bellman-Ford算法)解决负权边
# Bellman-Ford核心算法 # 对于一个包含n个顶点,m条边的图, 计算源点到任意点的最短距离 # 循环n-1轮,每轮对m条边进行一次松弛操作 # 定理: # 在一个含有n个顶点的图中,任意 ...
- 最短路径之Bellman-Ford——解决负权边
Bellman-Ford算法非常简单,核心代码四行,可以完美的解决带有负权边的图. for(k=1;k<=n-1;k++) //外循环循环n-1次,n为顶点个数 for(i=1;i<=m; ...
- Dijkstra算法与Bellman - Ford算法示例(源自网上大牛的博客)【图论】
题意:题目大意:有N个点,给出从a点到b点的距离,当然a和b是互相可以抵达的,问从1到n的最短距离 poj2387 Description Bessie is out in the field and ...
- uva 558 - Wormholes(Bellman Ford判断负环)
题目链接:558 - Wormholes 题目大意:给出n和m,表示有n个点,然后给出m条边,然后判断给出的有向图中是否存在负环. 解题思路:利用Bellman Ford算法,若进行第n次松弛时,还能 ...
- Bellman-ford算法与SPFA算法思想详解及判负权环(负权回路)
我们先看一下负权环为什么这么特殊:在一个图中,只要一个多边结构不是负权环,那么重复经过此结构时就会导致代价不断增大.在多边结构中唯有负权环会导致重复经过时代价不断减小,故在一些最短路径算法中可能会凭借 ...
随机推荐
- 20165101刘天野 2018-2019-2《网络对抗技术》Exp3 免杀原理与实践
20165101刘天野 2018-2019-2<网络对抗技术>Exp3 免杀原理与实践 1. 实践内容 1.1 正确使用msf编码器,msfvenom生成如jar之类的其他文件,veil- ...
- Metasploit – 内网连接
0x00 问题描述 在渗透测试时,metasploit往往作为后渗透工具,(因为远程溢出越来越少).我一般都是在获得一个webshell后,来使用metasploit进行信息采集,或者内网扫描等操作. ...
- PHP练习题二
1.抓取远程图片到本地,你会用什么函数? fsockopen, A 2.用最少的代码写一个求3值最大值的函数. function($a,$b,$c){* W0 z* u6 k+ e. L a: }5 ...
- 迁移cnblog博客
title: 迁移cnblog博客 date: 2018-03-18 categories: cnblogs tags: life 写博客最怕就是这种迁来迁去的,太麻烦了 还好老早就使用markdow ...
- maven中pom.xml标签介绍
pom作为项目对象模型.通过xml表示maven项目,使用pom.xml来实现.主要描述了项目:包括配置文件:开发者需要遵循的规则,缺陷管理系统,组织和licenses,项目的url,项目的依赖性,以 ...
- Git和GitHub相关
组员从GitHub上下载项目并上传项目的步骤如下 .组员接收到组长发的项目地址,组员需要从GitHub上把项目克隆下来,首先组员 需要在本地的一个文件夹里打开git,然后运行如下代码:git clon ...
- Django之ModelForm详解
前言 这是一个神奇的组件,通过名字我们可以看出来,这个组件的功能就是把model和form组合起来.先来一个简单的例子来看一下这个东西怎么用: 比如我们的数据库中有这样一张学生表,字段有姓名,年龄,爱 ...
- 端口被sysmtem占用
今天启动Apache的时候老是提示失败,很简单,使用 netstat -ano 发现80端口被占用.如图所示:
- 用Java编程计算出所有的"水仙花数"
题目:打印出所有的 "水仙花数 ",所谓 "水仙花数 "是指一个三位数,其各位数字立方和等于该数本身.例如:153是一个 "水仙花数 ",因 ...
- nrm npm源管理利器
nrm npm源管理利器 nrm是管理npm源的一个利器. 有时候我们用npm install 安装依赖时会非常的慢,是官方自身的npm本来就慢,然后我们会尝试安装淘宝的npm或者cnpm,这些安装切 ...
