[luogu3806]【模板】点分治1

description

求树上长度为\(k\)的路径是否存在。

data range

\[n\le 10000,k\le 10000000
\]

solution

点分治复习。。。

使用普通的点分治枚举路径模板即可。

一个小细节

本人初学点分治的时候是这样写的

int sum,rt,sz[N],w[N];bool vis[N];
void getrt(int u,int ff){//找到对应连通块的重心
  sz[u]=1;w[u]=0;
  for(RG int i=head[u];i;i=nxt[i]){
    RG int v=to[i];if(v==ff||vis[v])continue;
    getrt(v,u);sz[u]+=sz[v];
    w[u]=max(w[u],sz[v]);
  }
  w[u]=max(w[u],blk-sz[u]);
  if(w[rt]>w[u])rt=u;
}
void solve(int u){//递归分治
  vis[u]=1;
  for(RG int i=head[u];i;i=nxt[i]){
    RG int v=to[i];if(vis[v])continue;
    rt=0;blk=sz[v];
    getrt(v,0);
    solve(rt);
  }
}

int main()
{
    //...
    rt=0;w[0]=sum=n;
    getrt(1,0);
    solve(rt);
    return 0;
}

现在感觉这样写有问题。

关键出在直接赋值\(sum=sz[v]\)上。

给出一棵树:



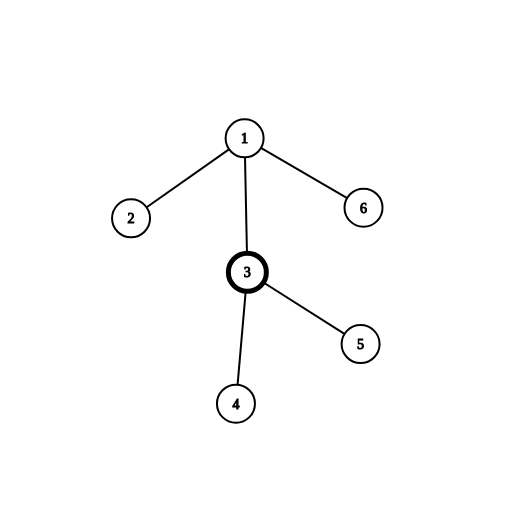
我们第一次选择的重心是节点\(3\)

然而这时\(sz[1]=6\)

于是我们递归解决上面部分的时候重心就会受到影响

然后就可能会\(T\)

解决方法是两边\(dfs\)像这样似乎常数又加大了:

int sum,rt,sz[N],w[N];bool vis[N];
void getrt(int u,int ff){//找到对应连通块的重心
  sz[u]=1;w[u]=0;
  for(RG int i=head[u];i;i=nxt[i]){
    RG int v=to[i];if(v==ff||vis[v])continue;
    getrt(v,u);sz[u]+=sz[v];
    w[u]=max(w[u],sz[v]);
  }
  w[u]=max(w[u],blk-sz[u]);
  if(w[rt]>w[u])rt=u;
}
void solve(int u){//递归分治
  vis[u]=1;
  for(RG int i=head[u];i;i=nxt[i]){
    RG int v=to[i];if(vis[v])continue;
    rt=0;blk=sz[v];
    getrt(v,0);
    getrt(rt,0);//第二遍dfs
    solve(rt);
  }
}

int main()
{
    //...
    rt=0;w[0]=sum=n;
    getrt(1,0);
    getrt(rt,0);//第二遍dfs
    solve(rt);
    return 0;
}

Code

#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<iomanip>
#include<cstring>
#include<complex>
#include<vector>
#include<cstdio>
#include<string>
#include<bitset>
#include<ctime>
#include<cmath>
#include<queue>
#include<stack>
#include<map>
#include<set>
#define Cpy(x,y) memcpy(x,y,sizeof(x))
#define Set(x,y) memset(x,y,sizeof(x))
#define FILE "a"
#define mp make_pair
#define pb push_back
#define RG register
#define il inline
using namespace std;
typedef unsigned long long ull;
typedef vector<int>VI;
typedef long long ll;
typedef double dd;
const int N=10010;
const int M=10000010;
const dd eps=1e-5;
const int inf=2147483647;
const ll INF=1ll<<60;
const ll P=100000;
il ll read(){
  RG ll data=0,w=1;RG char ch=getchar();
  while(ch!='-'&&(ch<'0'||ch>'9'))ch=getchar();
  if(ch=='-')w=-1,ch=getchar();
  while(ch<='9'&&ch>='0')data=data*10+ch-48,ch=getchar();
  return data*w;
}

il void file(){
  srand(time(NULL)+rand());
  freopen(FILE".in","r",stdin);
  freopen(FILE".out","w",stdout);
}

int n,m,rt,blk,k,flg;
int head[N],nxt[N<<1],to[N<<1],val[N<<1],cnt;
il void add(int u,int v,int w){
  to[++cnt]=v;val[cnt]=w;nxt[cnt]=head[u];head[u]=cnt;
}

int sz[N],w[N];bool vis[N],tong[M];
void getrt(int u,int ff){
  sz[u]=1;w[u]=0;
  for(RG int i=head[u];i;i=nxt[i]){
    RG int v=to[i];if(v==ff||vis[v])continue;
    getrt(v,u);sz[u]+=sz[v];
    w[u]=max(w[u],sz[v]);
  }
  w[u]=max(w[u],blk-sz[u]);
  if(w[rt]>w[u])rt=u;
}

int dep[N],cal[N],top;
void getdep(int u,int ff){
  cal[++top]=dep[u];
  for(RG int i=head[u];i;i=nxt[i]){
    RG int v=to[i];if(v==ff||vis[v])continue;
    dep[v]=dep[u]+val[i];if(dep[v]<=k)getdep(v,u);
  }
}
void getcl(int u,int ff){
  tong[dep[u]]=0;
  for(RG int i=head[u];i;i=nxt[i]){
    RG int v=to[i];if(v==ff||vis[v])continue;
    getcl(v,u);
  }
}
void solve(int u){
  vis[u]=1;dep[u]=0;cal[++top]=0;
  for(RG int i=head[u];i;i=nxt[i]){
    RG int v=to[i];if(vis[v])continue;
    dep[v]=dep[u]+val[i];getdep(v,u);
    for(RG int j=1;j<=top;j++)
      if(tong[k-cal[j]]||cal[j]==k)flg=1;
    for(RG int j=1;j<=top;j++)
      tong[cal[j]]=1;
    top=0;
  }
  getcl(u,0);
  for(RG int i=head[u];i;i=nxt[i]){
    RG int v=to[i];if(vis[v])continue;
    rt=0;blk=sz[v];
    getrt(v,0);
    getrt(rt,0);
    solve(rt);
  }
}

int main()
{
  n=read();m=read();
  for(RG int i=1,u,v,w;i<n;i++){
    u=read();v=read();w=read();
    add(u,v,w);add(v,u,w);
  }
  for(RG int i=1;i<=m;i++){
    k=read();flg=0;
    memset(vis,0,sizeof(vis));
    rt=0;blk=w[0]=n;
    getrt(1,0);
    getrt(rt,0);
    solve(rt);

    flg?puts("AYE"):puts("NAY");
  }
  return 0;
}