R数据分析第一篇：温习概率论

概率论是人们在长期实践中发现的理论，是客观存在的。自然界和社会上发生的现象是多种多样的，有一类现象，在一定条件下必然发生，称作确定性现象，而概率论研究的现象是不确定性现象，嗯嗯，醒醒，概率论研究的对象是随机现象。那什么是随机现象呢？在个别试验中呈现出不确定性，而在大量重复实验中呈现出固有规律性的现象，称作随机现象，在大量重复实验中所呈现的固有规律，是统计规律性，也就是概率。

一，概率和频率

在说概率之前，不得不说频率。对于一个随机事件来说，在一次试验中可能发生，也可能不发生，那么，如何表征事件在一次试验中发生的可能性大小呢？为了解答这个问题，引入了频率。频率描述了事件发生的频繁程度，频率越大，事件发生的越频繁，这意味着事件在一次试验中发生的可能性越大。我们定义，概率表征事件在一次试验中发生的可能性大小，因此，可从频率引出概率。

概率是事件的固有规律，必须是稳定的一个数值，频率具有稳定性吗？在长期实践中，当试验次数不断增大时，事件发生的频率稳定在一个值附近，这一客观事实证明频率具有稳定性。伯努利大数定理用数学公式证明了频率的稳定性，因此，在实际应用中，当试验次数很大时，可以用事件的频率来代替事件的概率，用于表征事件发生的可能性大小。

在大学概率论中，都学过正态分布。中心极限定理表明，在相当一般的条件下，当独立随机变量的个数不断增加时，其和的分布趋于正太分布，通俗地说，如果一个事件受到N（N趋近于无穷）个独立的因素的共同影响，且每个因素产生的影响都是独立的，那么这个事件发生的概率就服从中心极限定理，收敛于正态分布。在实际应用中，正态分布是非常重要的，只要影响因素充分多，都可以用正态分布来预测事件发生的概率。

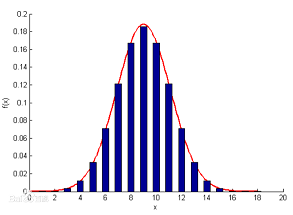
在研究概率论时，可以使用随机变量代表随机试验的一个结果，而这个随机变量具有数值属性，代表一个数值，这使得，可以使用数学分析的方法来描述随机现象。随机变量的取值随实验的结果而定，在试验之前不能预知事件的概率，且它的取值有一定的概率。在计算概率时，根据随机变量是否可以罗列，把随机变量分为离散型和连续型。

1，离散性随机变量

如果随机变量的全部取值是有限个或可列无限多个，这种随机变量称作离散性随机变量。离散性随机变量使用分布规律来研究，服从二项分布或泊松分布。要归纳一个离散型随机变量的统计规律，只需要知道随机变量的可能取值，以及每一个取值的可能值。也就是说，对于每一个可能的取值，都有一个数值来表征该值出现的可能性。

2，连续性随机变量

对于连续性随机变量，由于其可能的取值不能一一列举出来，通常情况下，连续性随机变量取某一个值的概率都是0。连续性随机变量使用概率密度来研究，服从概率密度函数。常用的概率密度是：均匀分布，指数分布和正态分布。概率密度是什么意思？简单来说，就是连续随机变量落在某个区间的面积就是其概率。

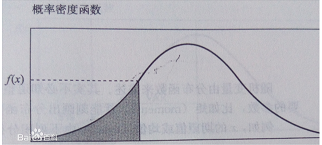
从坐标系上看，把概率密度看成是纵坐标，区间看成是横坐标，概率密度对区间的积分就是面积，而这个面积就是事件在这个区间发生的概率，所有区间的面积的和为1，因此，事件发生在某一个区间内的概率就是面积的大小。

二，随机变量的数字特征

对于单个随机变量，有两个描述性统计量：

数学期望，是随机变量的均值，是随机变量和概率的乘积的加和。
方差：表征随机变量和均值的偏离程度。

两个随机变量之间的线性关系：

协方差表征两个随机变量的变化相关程度。通俗地说，是两个变量在变化过程中是同方向变化（同时增大），还是反方向变化（一个增大，一个减小），以及变化的程度（数值越大，同向程度越大）。
相关系数，也称为线性相关系数，用于表征两个随机变量的线性变化的相关程度，如果相关系数是0，表示两个随机变量之间没有关系，不相关。

大学期间学习的统计知识，挥一挥手，都没有带走；闲来无事，温习一下，只摘重点，不求细节，能用就行。