[POI 2004]SZP

Description

Byteotian 中央情报局 (BIA) 雇佣了许多特工. 他们每个人的工作就是监视另一名特工.
Byteasar 国王需要进行一次秘密行动,所以他要挑选尽量多的信得过的特工. 但是这项任务是如此的机密以至于所有参加行动的特工都必须至少被另一名没有参加任务的特工所监视(就是说如果某个特工参加了行动,那么原先监视他的那些特工中至少要有一个没有参加进行动). 给出监视任务的详情,要求计算最多能有多少个特工参与其中.

Input

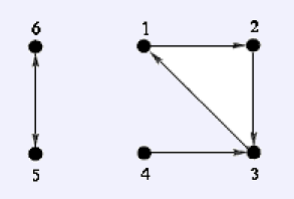
第一行只有一个整数, n – 特工的总数, 2 <= n <= 1000000. 特工从 1 到 n 编号. 接下来 n 行每行一个整数 ak 表示特工 k 将要监视特工 ak , 1 <= k <= n, 1 <= ak <= n, ak <> k.

Output

打印一个数,最多能有多少特工参加入这个任务.

Sample Input

6

2

3

1

3

6

5

Sample Output

3

HINT

题解

可以用贪心$+$拓扑排序做。

首先我们可以发现，入度为$0$的点必然不能被选，我们先将所有点标记为不选，将入度为$0$的点加入队列中。

由贪心的思想，我们为了被选的点更多，我们要将不选的点所指向的点选上。

证明：若点$i$确定为不选，若$ak[i]$不选也只能提供一个点被选（$ak[i]$指向的点），故$ak[i]$选上不会差。

若所有指向$i$的点均选，则$i$只能是不选。

由于图可能不连通还可能有环。我们只需要最后剩下的环从任意处切开即可。

由于我们在拓扑排序的过程中在环上做过标记。我们只要考虑没做过标记的一段，即有$i$标记为不选，$ak[i]$标记也为不选，显然我们要标记$ak[i]$为选。

 #include<map>
 #include<cmath>
 #include<ctime>
 #include<queue>
 #include<stack>
 #include<vector>
 #include<cstdio>
 #include<string>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #define LL long long
 #define Max(a,b) ((a)>(b) ? (a):(b))
 #define Min(a,b) ((a)<(b) ? (a):(b))
 using namespace std;
 const int N=;

 int n;
 int ak[N+];
 int in[N+];
 bool choose[N+],vis[N+];
 queue<int>Q;
 int ans;

 int Read()
 {
     int sum=;
     char c=getchar();
     while (c<''||c>'') c=getchar();
     while (c>=''&&c<='') sum=sum*+c-'',c=getchar();
     return sum;
 }

 int main()
 {
     scanf("%d",&n);
     for (int i=;i<=n;i++) ak[i]=Read(),in[ak[i]]++;
     for (int i=;i<=n;i++) if (!in[i]) Q.push(i);
     while(!Q.empty())
     {
         int u=Q.front();Q.pop();
         vis[u]=;
         if (choose[u])
         {
             in[ak[u]]--;
             if (!in[ak[u]]) Q.push(ak[u]);
         }
         else
         {
             if (!choose[ak[u]])
             {
                 choose[ak[u]]=;
                 ans++;
                 Q.push(ak[u]);
             }
         }
     }
     for (int i=;i<=n;i++) if (!vis[i])
     {
         vis[i]=;
         int j=i;
         while (!vis[ak[j]])
         {
             if (!choose[j]&&!choose[ak[j]]) ans++,choose[ak[j]]=;
             j=ak[j];vis[j]=;
         }
     }
     printf("%d\n",ans);
     return ;
 }