Linux下软链接与硬链接的区别

由于下面会说到inode，所以如果没有了解过，请务必搞懂inode的真正含义，厚颜无耻的推荐我的一篇博客：Linux磁盘与文件系统管理

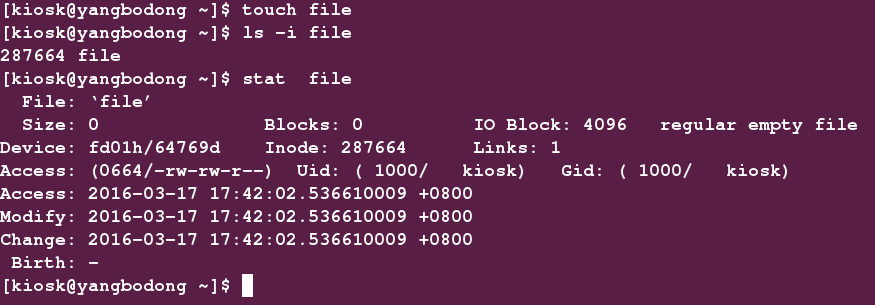
如果我们在系统中新建一个文件，我们看到的文件名实际上只是表面现象，本质上会分配一个inode给我们用，inode记录的信息有：文件的block位置，文件的UID，文件的GID，文件的读写执行权限等等，下面我们新建立一个名为file的文件。

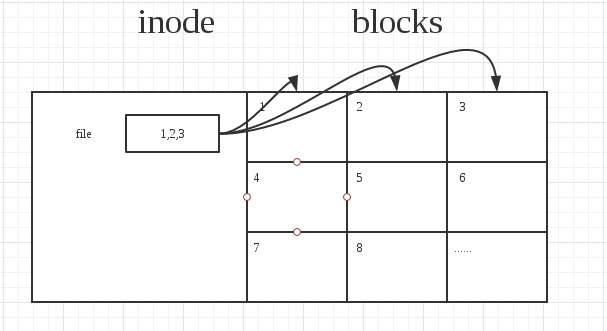
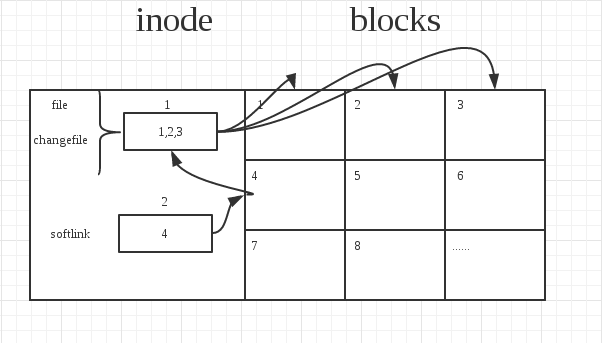
实际上file在我们系统中存在的样子更加形象的可以用下面的图片来表示：

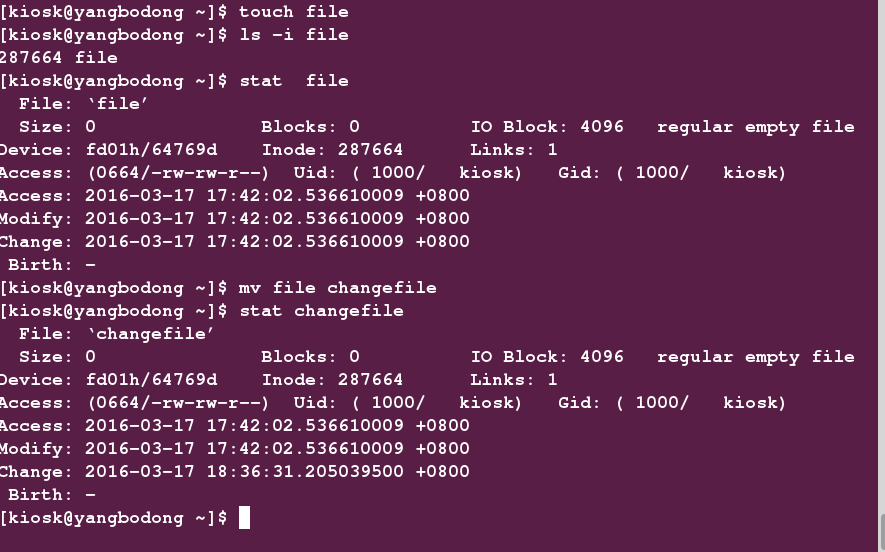
file只是个名字，我们可以用mv命令更改这个名字，它只是让我们用户好记，并且从我们的角度为它分配某些含义而已（比如我们习惯将密码文件命名为passwd）。

我们看到changefile和file是一模一样的，没有任何差别，所以也就是说文件名并不能反映一个文件的属性。接下来我们就要说重点，软链接和硬链接了。

硬链接

硬链接实际上是一个文件inode的别名，我们可以为一个inode起很多个名字，同时让file和changefile存在也是可以的，就是建立硬链接，因为文件名不会对文件本身产生影响。

ln 命令可以用来建立链接,不加参数表示建立硬链接
-s：建立软链接

下面我们给changefile建立硬链接file，将我们的file找回来。

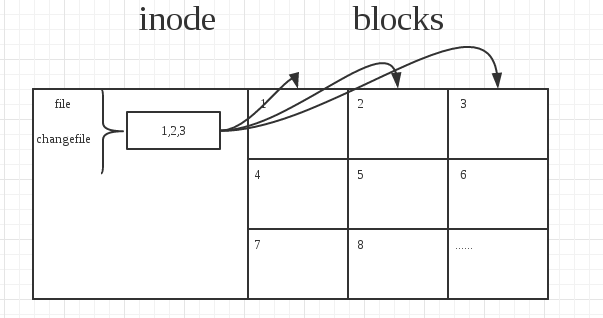
通过ls -i命令查看inode我们发现它们是一样的，那么目前的情况会是怎样呢？如下：

只不过就是此inode有两个名字了而已，我们通过任意一个文件名查看或者修改文件的内容，都会直接查看或者修改blocks块中1,2,3的内容，并且file和changefile之间是不会互相影响的，我们删除任何一个对对方没有任何影响，大不了就是inode少一个名称而已。

软链接

与硬链接不同，软链接相当于快捷方式，当我们双击一个图标打开一个软件时，本质上是在执行一个.exe文件一样，通过这个图标只能找到这个.exe文件，执行的过程是.exe完成的，如果.exe找不到，那么这个快捷方式将会失效。因此在linux中的软链接实际上是另一个文件，这个文件与原文件是不同的，唯一的特殊之处就是它的内容记录的是原文件的inode,我们通过inode再来找原文件的位置。

明显，softlink和changefile就是不同的文件。它的详细情况就像下面这样：

我们通过softlink会找到inode1的位置，然后通过它定位文件的block,因此，如果一旦inode1被删除了，那么softlink就会无法找到文件，也就是这个软链接会失效。我们删除changefile试试看：

[kiosk@yangbodong ~]$ echo hello > file   //给file中写入hello
[kiosk@yangbodong ~]$ cat file changefile softlink //三个文件中都有hello
hello
hello
hello
[kiosk@yangbodong ~]$ rm -fr file  //删除了file
[kiosk@yangbodong ~]$ cat softlink //由于目前changefile还存在，inode1存在，因此softlink是有效的
hello
[kiosk@yangbodong ~]$ rm -fr changefile //删除了changefile
[kiosk@yangbodong ~]$ cat softlink  //目前softlink再也找不到原来的inode的位置，因此失效了。
cat: softlink: No such file or directory

软链接和硬链接的比较

	软链接	硬链接
优点	可以对目录创建	安全，节省空间
缺点	消耗inode	不能对目录创建，不能跨越文件系统