Codeforces 450B div.2 Jzzhu and Sequences 矩阵快速幂or规律

Jzzhu has invented a kind of sequences, they meet the following property:

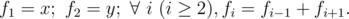
You are given x and y, please calculate fn modulo 1000000007 (109 + 7).

Input

The first line contains two integers x and y (|x|, |y| ≤ 109). The second line contains a single integer n (1 ≤ n ≤ 2·109).

Output

Output a single integer representing fn modulo 1000000007 (109 + 7).

Examples

input

2 3
3

output

1

input

0 -1
2

output

1000000006

Note

In the first sample, f2 = f1 + f3, 3 = 2 + f3, f3 = 1.

In the second sample, f2 =  - 1;  - 1 modulo (109 + 7) equals (109 + 6).

题意：给出一个递推式和前两项，求第n项模1e9+7后的值。

题解：这题其实本来是很水的..只是最近都在尝试写一些矩阵快速幂的题目，最难的在于化递推式并构造矩阵上，而这道题直接给出了递推式，心痒想使用矩阵。_(:3」∠)_

由f(i)=f(i+1)+f(i-1)可以得出f(i+1)=f(i)-f(i-1)

又由于i>=2，从f(1)开始，于是

f(3)=(1) * f(2) + (-1) * f(1)

f(2)=(1) * f(1) + (0) * f(0)

另外要注意的是，得到的值是负数还得再处理一下。（最近总WA在这上）

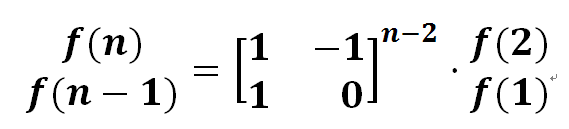
 #include <stdio.h>
 #include <algorithm>
 #include <iostream>
 #include <string.h>
 #define ll __int64
 using namespace std;

 const int mod = ;
 struct matrix
 {
     ll x[][];
 };
 matrix mul(matrix a, matrix b)
 {
     matrix c;
     c.x[][] = c.x[][] = c.x[][] = c.x[][] = ;
     for( int i = ; i < ; i++)
         for(int j = ; j < ; j++)
         {
             for(int k = ; k < ; k++)
             {
                 c.x[i][j] += a.x[i][k] * b.x[k][j];
             }
             c.x[i][j] %= mod;
         }
     return c;
 }
 matrix powe(matrix x, ll n)
 {
     matrix r;
     r.x[][] = r.x[][] = ;  //注意初始化
     r.x[][] = r.x[][] = ;
     while(n)
     {
         if(n & )
             r = mul(r , x);
         x = mul(x , x);
         n >>= ;
     }
     return r;
 }
 int main()
 {

     ll x, y, n, ans;
     while(~scanf("%I64d%I64d%I64d", &x, &y, &n))
     {
         if(n == )
             printf("%I64d\n",(y%mod + mod)%mod);  //负数情况下的考虑
         else if(n == )
             printf("%I64d\n",(x%mod + mod)%mod);
         else
         {
             matrix d;
             d.x[][] = ;
             d.x[][] = -;
             d.x[][] = ;
             d.x[][] = ;

             d = powe(d, n - );
             ans = d.x[][] * y +d.x[][]*x;
             printf("%I64d\n", (ans%mod+mod)%mod );
         }

     }
 }