python解决组合问题
1.问题描述
比如9个数中取4个数的组合以及列出各种组合,该如何做?
我们可以考虑以下一个简单组合:从1,2,3,4,5,6中,如何选取任意四个数的组合。
固定:1 2 3 ,组合有1234 1235 1236
固定1 2 4,组合有:1245 1246
固定1 2 5,组合有:1256
固定1 3 4,组合有:1345 1346
固定1 3 5,组合有:1356
固定1 4 5,组合有:1456
固定2 3 4,组合有:2345 2346
固定2 3 5,组合有:2356
固定2 4 5,组合有:2456
固定3 4 5,组合有:3456
共有15种组合
2.简单实现一下组合算法
首先,我们分析上面列出的10个步骤,对于1),很明显,在固定了1 2 3这三个数之后,第四个数就是4、5、6三个数进行了循环(还记得循环吗,计算机最拿手的就是做循环)。其次,我们再分析1)2)3)这三个步骤中固定的数字,前两个没有变,都是1 2,只是第三个数在进行循环(又是循环)。
通过分析,我们可以找到这样的规律:
1 先固定3个数,让第四个数进行循环
2 让第三个数循环,重复第一步
3 让第二个数循环,重复第一步
4 让第一个数循环,重复第一步
def combNumberLoop4(m, b):
totalNumber = 0
for i in range(1, m+2-4):
b[0] = i
for j in range(i+1, m+2-3):
b[1] = j
for k in range(j+1, m+2-2):
b[2] = k
for l in range(k+1, m+2-1):
b[3] = l
print b
totalNumber += 1
return totalNumber group=[99,99,99,99]
print "\nUsing Loop: %d\n" % combNumberLoop4(6, group)
程序的输出结果,正如之前分析的那样。
3.如何递归解决组合问题
我们再回到C(6,4)问题,除了上面列出的十个步骤,我们换个思路:
如果在6个数中选定一个数,那么确定剩下的3个数是不是变为了“从5个数中选3个数的组合问题”了呢?以此类推,这似乎变成了一个“递归”问题了,确实,我们可以用递归的思路来解决这个问题。
对于C(m, n)列出所有组合的问题,可以按照一下的步骤来进行编程,这次我们按从后往前的顺序来列出所有组合:
1 选定一个元素i,在范围[m, n]内进行循环
2 将i 作为所求组合的最后一个元素
3 如果n-1>0,进行递归调用,求C(m-1, n-1);否则,输出结果
4 重复①
注意,设计递归函数一定要有终止条件,否则会造成“死循环”。
实现的代码如下:
def combNumber(m, n, b):
global totalNumberR
for i in range(m, n-1, -1):
b[n-1] = i
if n-1>0:
combNumber(i-1,n-1,b)
else:
print b
totalNumberR += 1
return totalNumberR group=[99,99,99,99,99]
totalNumberR = 0
print "\nUsing Recursive: %d\n" % combNumber(7,5,group)
递归的使用,让程序写起来非常的简洁,但是,在写程序的时候,我有两个地方(其实程序也就难在这两个地方),折腾了好几天才弄清楚:
首先是for循环的循环范围如何确定;
其次是递归调用时使用的参数设计;
3.python提供的内置组合函数
def combinations_with_replacement(iterable, r):
# combinations_with_replacement('ABC', 2) --> AA AB AC BB BC CC
pool = tuple(iterable)
n = len(pool)
if not n and r:
return
indices = [0] * r
yield tuple(pool[i] for i in indices)
while True:
for i in reversed(range(r)):
if indices[i] != n - 1:
break
else:
return
indices[i:] = [indices[i] + 1] * (r - i)
yield tuple(pool[i] for i in indices)
4.更多组合算法
请点击我:https://docs.python.org/3/library/itertools.html?highlight=combinations#itertools.combinations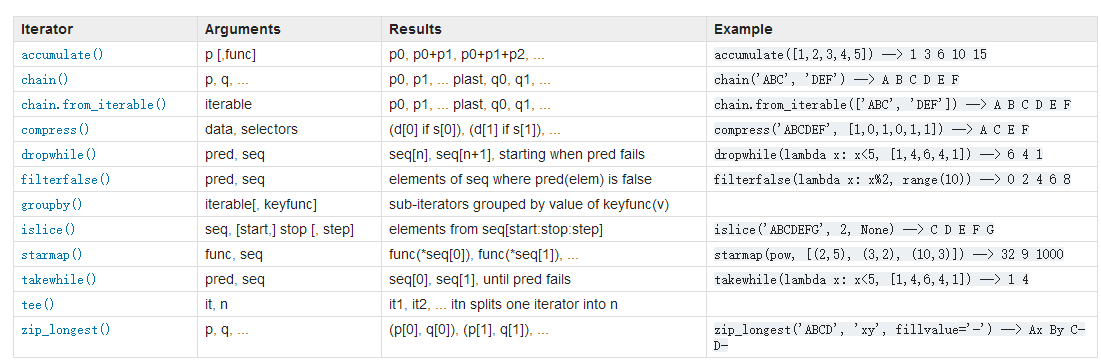
python解决组合问题的更多相关文章
- C# 解决组合优化问题
Google Optimization Tools介绍 Google Optimization Tools(OR-Tools)是一款专门快速而便携地解决组合优化问题的套件.它包含了: 约束编程求解器. ...
- python笔记-用python解决小学生数学题【转载】
本篇转自博客:上海-悠悠 原文地址:http://www.cnblogs.com/yoyoketang/tag/python/ 前几天有人在群里给小编出了个数学题: 假设你有无限数量的邮票,面值分别为 ...
- python的组合数据类型及其内置方法说明
python中,数据结构是通过某种方式(例如对元素进行编号),组织在一起数据结构的集合. python常用的组合数据类型有:序列类型,集合类型和映射类型 在序列类型中,又可以分为列表和元组,字符串也属 ...
- 《用Python解决数据结构与算法问题》在线阅读
源于经典 数据结构作为计算机从业人员的必备基础,Java, c 之类的语言有很多这方面的书籍,Python 相对较少, 其中比较著名的一本 problem-solving-with-algorithm ...
- 有关科学计算方面的python解决
在科学计算方面,一般觉得matlab是一个超强的东西.此外还有R. 至于某种语言来说,一般都要讲究一些特别的算法,包含但不限于: 矩阵方面的计算 指数计算 对数计算 多项式运算 各类方程求解 总之.仅 ...
- appium+python解决每次运行代码都提示安装Unlock以及AppiumSetting的问题
appium+python解决每次运行代码都提示安装Unlock以及AppiumSetting的问题(部分安卓机型) 1.修改appium-android-driver\lib下的android-he ...
- 高德API+Python解决租房问题(.NET版)
源码地址:https://github.com/liguobao/58HouseSearch 在线地址:58公寓高德搜房(全国版):http://codelover.link:8080/ 周末闲着无事 ...
- Python的组合模式与责任链模式编程示例
Python的组合模式与责任链模式编程示例 这篇文章主要介绍了Python的组合模式与责任链模式编程示例,组合模式与责任链模式都属于Python的设计模式,需要的朋友可以参考下 组合模式 我们把Com ...
- python的组合数据
python的组合数据包括:1.列表list[ ] 2.元组tuple(),3.字典dict{"x":"y"},4.集合set{} 1.创造组合数据:均可直 ...
随机推荐
- JVM调优总结(6):新一代的垃圾回收算法
垃圾回收的瓶颈 传统分代垃圾回收方式,已经在一定程度上把垃圾回收给应用带来的负担降到了最小,把应用的吞吐量推到了一个极限.但是他无法解决的一个问题,就是Full GC所带来的应用暂停.在一些对实时性要 ...
- IFeatureCursorProxy.flush AutomationException: 0x80041538
添加面的时候碰到的一个问题,有些数据没问题,有些报错,后来请教一位同事说有可能是经纬度字段的数据精度问题,因为投影坐标系统不同,支持的经纬度经度不同,后来转换投影坐标系统后果然解决问题了,我一开始也怀 ...
- CodeForces - 1003D
Polycarp has nn coins, the value of the ii-th coin is aiai. It is guaranteed that all the values are ...
- spring-boot 更换依赖版本
创建Spring Boot操作步骤如下: 在File菜单里面选择 New > Project,然后选择Spring Initializr 更换版本 或 pom spring-boot-start ...
- perl6正则 3: 行开头与结尾与多行开头,多行结尾
^ $ 匹配一行的开头或结尾, 可以用 ^ 或 $. > so 'abcde' ~~ /e$/ True > so 'abcdef' ~~ /e$/ False > so 'abcd ...
- dm368 ipnc3.0环境搭建脚本
前言 为了方便其他人搭建dm368 ipnc3.0环境,我写了个脚本,执行脚本就可以自动搭建好环境了,绝对的傻瓜操作了,不过有一个地方让我很郁闷,那就是在用sed替换掉某段内容的时候(143行--15 ...
- UOJ#58/BZOJ 3052【WC2013】糖果公园
好写好调的莫队算法,就算上树了仍然好写好调. 传送门 http://uoj.ac/problem/58 简要做法 将树按照dfs序分块,然后将询问按照(u所在块,v所在块,时间)作为关键字进行排序,依 ...
- hdu 2852 KiKi's K-Number (线段树)
版权声明:本文为博主原创文章,未经博主允许不得转载. hdu 2852 题意: 一个容器,三种操作: (1) 加入一个数 e (2) 删除一个数 e,如果不存在则输出 No Elment! (3) 查 ...
- learnyounode 题解
//第三题 var fs =require('fs')var path=process.argv[2]fs.readFile(path,function(err,data){ var lines=da ...
- Shp上传至Oracle Spatial
1.下载shp2sdo,将shp文件拷贝至shp2sdo相同路径下,打开windows命令窗口,执行: shp2sdo shp文件名 表名 -i id -s 4326 -d 例如:shp2sdo ci ...
