Python多继承的C3算法

C3算法

一、知识点补充：

拓扑排序：在图论中，拓扑排序(Topological Sorting) 是一个 有向无环图(DAG,Directed Acyclic Graph) 的所有顶点的线性序列。且该序列必须满足下面两个条件：

1. 每个顶点出现且只出现一次

2. 若存在一条从顶点A到顶点B的路径，那么在序列中顶点A出现在顶点B的前面，如下图：

显然它是DAG图，那么如何进行拓扑排序那？

1.从DAG途中选择一个没有前驱(即入度为0)的顶点并输出
2.从图中删除该顶点和所有以它为起点的有向边。
3.重复1和2直到当前DAG图为空或当前途中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。

最终，得到拓扑排序的结果是{1,2,4,3,5}

二、C3算法解析

1. 在python2中，默认选择深度优先的算法查找，只要继承object变成新式类才能广度优先,使用inspect.getmro()查看mro顺序, 在python3中直接 类.__mro__查看

import inspect
class A:
    def show(self):
        print "A.show()"
​
class B(A): pass
class C(A):
    def show(self):
        print "C.show()"
class D(B, C): pass
print inspect.getmro(D)  #(<class __main__.D at 0x105f0a6d0>, <class __main__.B at 0x105f0a600>, <class __main__.A at 0x105f0a668>, <class __main__.C at 0x105f0a738>)
print x.show()  # A.show()

python调用mro的方法

1. mro:method resolution order,主要用于在多继承时判断调的属性的路径(来自于哪个类)。mro是基于深度优先搜索算法的。在Python2.3之前是基于此算法，但从Python2.3起应用了新算法:C3算法.

2. C3算法的本质就是Merge(融合），不断地把mro()函数返回的序列进行Merge，规则如下：

   • 如果第一个序列的第一个元素，是后续序列的第一个元素，或者不在后续序列中再次出现，则将这个元素合并到最终的方法解析顺序序列中，并从当前操作的全部序列中删除。

   • 如果不符合，则跳过此元素，查找下一个列表的第一个元素，重复1的判断规则

   算法详解：C3 算法：MRO是一个有序列表L，在类被创建时就计算出来。

   L（Child（Base1，Base2））= [ Child + merge（ L（Base1）,L（Base2）,Base1Base2 ）]
   
   L（object）= [ object ]
   
   规则：
   
    L的性质：结果为列表，列表中至少有一个元素即类自己。
    +： 添加到列表的末尾，即 [ A + B ] = [ A，B ]
   
   ① 如果列表空则结束，非空，读merge中第一个列表的表头，
   ② 查看该表头是否在merge中所有列表的表尾中。
   ②-->③ 不在，则放入最终的L中，并从merge中的所有列表中删除，然后回到①中
   ②-->④ 在，查看当前列表是否是merge中的最后一个列表
   ④-->⑤ 不是，跳过当前列表，读merge中下一个列表的表头，然后回到 ②中
   ④-->⑥ 是，异常。类定义失败。
   
   # 表头： 列表的第一个元素 （列表：ABC，那么表头就是A,B和C就是表尾）
   # 表尾： 列表中表头以外的元素集合（可以为空）

   C3算法公式

   

   L(D) = L(D(O))
        = D + merge(L(O))
        = D + O
        = [D,O]
   L(B) = L(B(D,E))
        = B + merge(L(D) , L(E))
        = B + merge(DO , EO) # 第一个列表DO的表头D，其他列表比如EO的表尾都不含有D，所以可以将D提出来，即D是合法表头
        = B + D + merge(O , EO) #从第一个开始表头是O,但是后面的列表EO的表尾中含有O所以O是不合法的，所以跳到下一个列表EO
        = B + D + E + merge(O , O)
        = [B,D,E,O]
   同理:
   L(C) = [C,E,F,O]
   ​
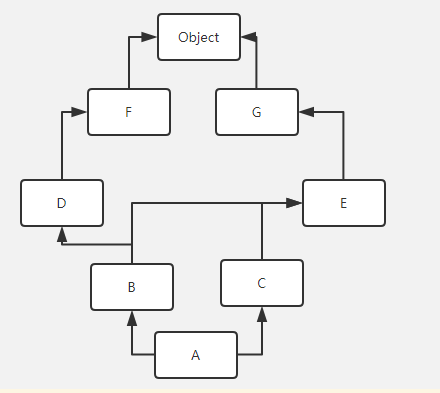
   L(A(B,C)) = A + merge(L(B),L(C),BC)
             = A + merge(BDEO,CEFO,BC) # B是合法表头
             = A + B + merge(DEO,CEFO,C) # D是合法表头
             = A + B + D + merge(EO,CEFO,C) # E不是合法表头，跳到下一个列表CEFO，此时C是合法表头
             = A + B + D + C + merge(EO,EFO) # 由于第三个列表中的C被删除，为空，所以不存在第三个表，只剩下两个表；此时E是合法表头
             = A + B + D + C + E + merge(O,FO) # O不是合法表头，跳到下一个列表FO，F是合法表头，
             = A + B + D + C + E + F + merge(O,O) # O是合法表头
             = A + B + D + C + E + F + O
             = [A,B,D,C,E,F,O]

   运算过程

三、C3算法例子

L(G)=L(G(o))
    =G + merge(L(o))
    =G + o
    =[G,o]
L(F)=L(F(G(o)))
    =F + merge(L(G))
    =F + Go
    =[F,G,o]
L(B)=L(B(F(G(o))))
    =B + merge(L(F(G(o))))
    =[B,F,G,o]
# 同理
 L(E)=L(E(o)) =[E,o]
 L(C)=L(C(E(o))) = [C,E,o]
 L(D)=L(D(G(o))) =[D,G,o]
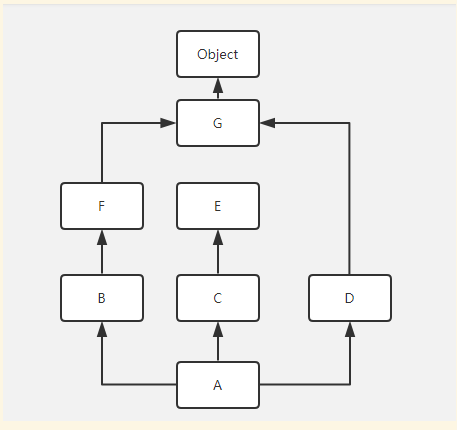
 L(A(B,C,D))=A +merge(L(B),L(C),L(D),BCD)
           =A +merge(BFGo,CEo,DGo,BCD) # B合法，实在第一元素，且也是尾部第一
           =A+B+merge(FGo,CEo,DGo,CD) # F合法，不再其他中出现
           =A+B+F+merge(Go,CEo,DGo,CD) # G不合法，出现两次，跳到下一个列表即第二个中，C满足
           =A+B+F+C+merge(Go,Eo,DGo,D) # E合格
           =A+B+F+C+E+merge(Go,o,DGo,D) # 跳至第三列，D满足
           =A+B+F+C+E+D+merge(Go,o,Go) # 目前Go为尾，所以G合法
           =A+B+F+C+E+D+G+merge(o,o,o)
           =A+B+F+C+E+D+G+o

运算过程

L(G)=L(G(o))=[G,o]
L(E)=L(E(G(o)))
    =E +merge(L(G(o)))
    =E+[G,o]=[E,G,o]
L(D)=L(D(o))=[D,o]
L(F)=L(F(o))=[F,o]
L(B)=L(B(D,E))=B+merge(L(D),L(E),DE)
             =B+merge(Do,EGo,DE) #D 合格
              =B +D +merge(o,EGo,E) # E合格
              =B +D + E +merge(G,o,)= [B,D,E,G,o]
L(C)=L(C(D,F))=C+merge(L(D),L(F),DF)
             =C+merge(Do,Fo,DF) #D 合法
              =C+D+merge(o,Fo,F)  # F合法
              =C+D+F+merge(o)=[C,D,F,o]
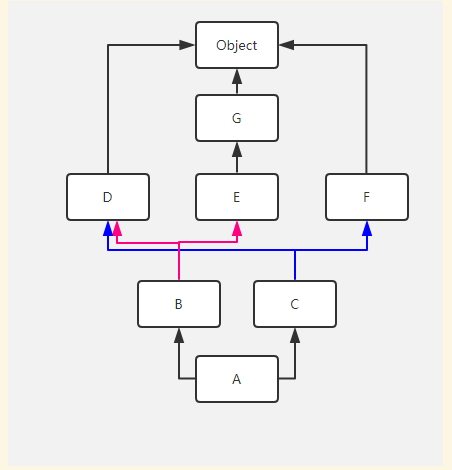
L(A)=L(A(B,C))=A+merge(L(B),L(C),BC) =A +merge(BDEGo,CDFo,BC)  #B合法
                                     =A + B+merge(DEGo,CDFo,C)  # D不合法，看第二元素C合格
                                  =A + B+C+merge(DEGo,DFo,) #D合格
                                   =A + B+C+D+merge(EGo,Fo,)# E合格
                                    =A + B+C+D+E+merge(Go,Fo,)
                                      =A + B+C+D+E+G+F+o=[A,B,C,D,E,G,F,o]

运算代码

L(F)=L(F(o))=[F,o]
L(G)=L(G(o))=[G,o]
L(D(F(o)))=[D,F,o] # 因为单向所以简单
L(E(G(o)))=[E,G,o]
L(B)=L(B(D,E))=B+merge(L(D),L(E))=B+merge(DFo,EGo,DE) # D合格
             =B+D+merge(Fo,EGo,E)  #F合格
              =B+D+F+merge(o,EGo,E)  # o不合格，E合格
              =B+D+F+E+merge(o,Go，) # G合格
              =[B,D,F,E,G,o]
L(C)=L(C(E(G(o))))=C +merge(L(E))=[C,E,G,o]
L(A)=L(A(B,C))=A+merge(L(B)+L(C))=A+merge(BDFEGo,CEGo,BC) #B合格
                                 =A+B+merge(DFEGo,CEGo,C) #D 合格
                                 =A+B+D+merge(FEGo,CEGo,C) #F合格
                                  =A+B+D+F+merge(EGo,CEGo,C) #E不合格 C合理
                                  =A+B+D+F+C+merge(EGo,EGo,) # 后面都一样了所以直接写
                                  = [A,B,D,F,C,E,G,o]

运算代码

四、多继承例子：

class A(object):
    def foo(self):
        print('A foo')
    def bar(self):
        print('A bar')
​
class B(object):
    def foo(self):
        print('B foo')
    def bar(self):
        print('B bar')
​
class C1(A):
    pass
​
class C2(B):
    def bar(self):
        print('C2-bar')
​
class D(C1,C2):
    pass
​
if __name__ == '__main__':
    print(D.__mro__)
    d=D() #  (<class '__main__.D'>, <class '__main__.C1'>, <class '__main__.A'>, <class '__main__.C2'>, <class '__main__.B'>, <class 'object'>)
    d.foo() # A foo
    d.bar()  # A bar

# 讲解：
#找到入度为0的顶点，只有一个D，拿D，剪掉D相关的边
#得到两个入度为0的顶点(C1,C2),根据最左原则，拿C1，剪掉C1相关的边，这时候序列为{D,C1}
#接着看，入度为0的顶点有两个(A,C1),根据最左原则，拿A，剪掉A相关的边，这时候序列为{D,C1,A}
#接着看，入度为0的顶点为C2,拿C2，剪掉C2相关的边，这时候序列为{D,C1,A,C2}
#继续，入度为0的顶点为B，拿B，剪掉B相关的边，最后还有一个object
#所以最后的序列为{D,C1,A,C2,B,object}
#以上参考：https://www.jianshu.com/p/c9a0b055947b （感谢）

多继承讲解

五、例题

# 判断下列题的运行结果
class Foo:
      def __init__(self):  # 来父类初始化，但是slef的本身有func函数
             self.func()
      def func(self):
             print(‘in foo’)
class Son(Foo):
      def func(self):
             print(‘in son’)
Son()     # 'in son'
 

例题