[CSP-S模拟测试]:Park（树上DP）

题目描述

　　公园里有$n$个雕像，有$n-1$条道路分别连接其中两个雕像，任意两个雕像可以直接或间接相连。现在每个景点$i$聚集着$P_i$只鸽子，旅行家手里有$v$数量的面包屑。
　　一旦旅行家在雕像$i$撒下$1$单位面包屑，那么相邻的雕像的鸽子就都会飞到雕像$i$来觅食。
　　时间线是这样的：首先，旅行家到达雕像$i$并与$P_i$鸽子会面。然后，他放下$1$单位面包屑。他离开雕像。在旅行家到达下一座雕像之前，来自相邻雕像的鸽子移动到雕像$i$（所以这些鸽子不计入他遇到的鸽子数）。注意旅行家每到一达雕像可以撒下面包屑，也可以不撒。
　　旅行家可以在任何一座雕像上进入公园，沿着一些道路走下去（但不要使用同一道路两次），然后离开公园。
　　在旅行家离开公园后，没有面包屑的小学生将进入并穿越完全相同的路线，并遇见许多群鸽子。
　　通过最多$v$单位面包屑，旅行家希望最大化旅行家在路线上遇到的鸽子数量与小学生遇到的鸽子数量之间的差异。

---

输入格式

第一行两个整数$n,v$
第二行$n$个数为$P_i$
接下来$n-1$，每行两个整数，$X_i,Y_i$表示$X_i$与$Y_i$雕像相连

---

输出格式

输出只有一行，表示答案

---

样例

样例输入：

12 2
2 3 3 8 1 5 6 7 8 3 5 4
2 1
2 7
3 4  
4 7  
7 6  
5 6  
6 8  
6 9
7 10
10 11
10 12

样例输出：

36

---

数据范围与提示

样例解释：

一个可行的方案：旅行家从雕像$6$进入公园。在那里他遇到了$5$只鸽子。他放下面包屑。$p_6$现在是$27$，$p_5=p_7=p_8=p_9=0$。接下来，他跑向雕像$7$并遇到$0$鸽子。他撒下了第二个面包屑。$p_7=41$且$p_2=p_4=p_6=p_{10}=0$。他离开公园，他总共遇见$5+0=5$只鸽子。小学生跟着他走过同样的路线，但遇到$p_6+p_7=0+41=41$只鸽子。差是$41-5=36$。

数据范围：

对于$20\%$的数据，$1\leqslant n\leqslant 10$
对于另外$20\%$的数据，$1\leqslant n\leqslant 1,000$
对于另外$30\%$的数据，存在一个可行的最优方案从$1$出发
对于另外$30\%$的数据无特殊限制
对于$100\%$的数据，$1\leqslant n\leqslant 10^5,0\leqslant v\leqslant 100,0\leqslant P_i\leqslant 10^9$

---

题解

原题见$CEOI2017\ Chase$，我也不知道玄学出题人改的什么玄学题面……

一看就是$DP$题，但是显然我们不能枚举起点。

但是我们还是要先想一下枚举端点的做法，做事要慢慢来～

我的做法是设$dp[i][j][0/1]$表示到了$i$号点，已经撒了$j$次，在当前节点有没有撒的最大收益，转移是这样的：

$$dp[i][j][0]=max(dp[fa][j][0],dp[fa][j][1]) \\ dp[i][j][1]=max(dp[fa][j-1][0],dp[fa][j-1][1])+sum[i]-p[fa]$$

其中$sum[i]$表示在$i$号点撒会引来$sum[i]$只鸽子，不含$i$号点本身就有的，如下图$\downarrow$

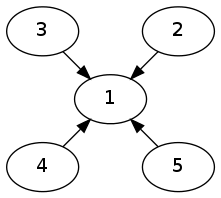
$sum[i]$是指$\sum \limits_{i=1}^4 p_i$。

直接这样做会$TLE\ 44$，如果我们加上$clock()$的话可以得到$74\sim 78$不等。

那么我们现在考虑满分解法，如何快速求出以每个点为起点的最大贡献，将其取$\max$即可。

考虑定义两个数组$up[i][j]$和$down[i][j]$分别表示从$i$的子树走向$i$和从$i$走向$i$的子树，撒了$j$次的最大贡献。

然后状态转移是这样的：

$$up[i][j]=\max(up[i][j],up[son][j],up[son][j-1]+sum[i]-p[son]) \\ down[i][j]=\max(down[i][j],down[son][j],down[son][j-1]+sum[i]-p[fa])$$

还需要注意一点，如下图$\downarrow$

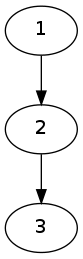
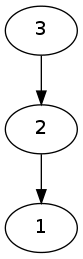
两种走法的最大贡献不一定相等，于是我们要正序枚举一遍所有的儿子，再倒着枚举一遍即可。

时间复杂度：$\Theta(n\times v)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
int n,v;
int p[100001];
long long sum[100001];
long long dp[2][100001][101];
long long ans;
vector<int> e[100001];
void dfs(int x,int fa)
{
	for(int i=1;i<=v;i++)
	{
		dp[0][x][i]=sum[x];
		dp[1][x][i]=sum[x]-p[fa];
	}
	for(int i=0;i<e[x].size();i++)
		if(e[x][i]!=fa)
		{
			dfs(e[x][i],x);
			for(int j=1;j<v;j++)ans=max(ans,dp[0][x][j]+dp[1][e[x][i]][v-j]);
			for(int j=1;j<=v;j++)
			{
				dp[0][x][j]=max(dp[0][x][j],max(dp[0][e[x][i]][j],dp[0][e[x][i]][j-1]+sum[x]-p[e[x][i]]));
				dp[1][x][j]=max(dp[1][x][j],max(dp[1][e[x][i]][j],dp[1][e[x][i]][j-1]+sum[x]-p[fa]));
			}
		}
	reverse(e[x].begin(),e[x].end());
	for(int i=1;i<=v;i++)
	{
		dp[0][x][i]=sum[x];
		dp[1][x][i]=sum[x]-p[fa];
	}
	for(int i=0;i<e[x].size();i++)
		if(e[x][i]!=fa)
		{
			for(int j=1;j<v;j++)ans=max(ans,dp[0][x][j]+dp[1][e[x][i]][v-j]);
			for(int j=1;j<=v;j++)
			{
				dp[0][x][j]=max(dp[0][x][j],max(dp[0][e[x][i]][j],dp[0][e[x][i]][j-1]+sum[x]-p[e[x][i]]));
				dp[1][x][j]=max(dp[1][x][j],max(dp[1][e[x][i]][j],dp[1][e[x][i]][j-1]+sum[x]-p[fa]));
			}
		}
	ans=max(ans,max(dp[0][x][v],dp[1][x][v]));
}
int main()
{
	scanf("%d%d",&n,&v);if(!v){puts("0");return 0;}
	for(int i=1;i<=n;i++)scanf("%d",&p[i]);
	for(int i=1;i<n;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		e[x].push_back(y);
		e[y].push_back(x);
		sum[x]+=p[y];
		sum[y]+=p[x];
	}
	dfs(1,0);
	printf("%lld",ans);
	return 0;
}

---

rp++