codeforces 1156E Special Segments of Permutation

题目链接：https://codeforc.es/contest/1156/problem/E

题目大意：

在数组p中可以找到多少个不同的l,r满足。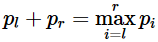

思路：

ST表+并查集。

ST表还是需要的，因为nlongn的预处理就可以O(1)查询。枚举所有的区间也就O(n^2)。

因为是输入固定1-n,所以我可以设一个y数组表示数组p的值所对应的下标。

(习惯输入为x数组)

我们考虑一个区间[l,r]这个区间最大值为i。(这里用ST表可以找到)

[l,r]对答案的贡献为最大值i左边找一个值a,右边找一个值b,满足a+b==i。有多少个不同的a,b对。

我们可以枚举i左右两边长度小的区间。然后在大区间上找。(小区间就可以少枚举点不是吗？最坏左右区间长度一样总共也就nlongn次)。

然后的问题是怎样找快速查找。

我们用并查集。

把大区间的所有值加入在大区间的最大值上。

你一定疑惑这样做还是会超时的啊。

如果在我们得到这个区间对答案的贡献后，把i左右两区间的最大值加在i上就可以完美的解决这个问题了。

我们直接从区间[1,n]开始，向下遍历，稍微注意一下边缘条件就OK啦。

整个就像一个线段树呢。

人太垃圾，ST表直接复制的板子，如有抄袭希望可以交个朋友哈~~

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(false);
#define int long long
#define N 200100
#define mod 1000000007

int x[N];
int y[N];

int pre[N];
int find(int x)
{
    int r=x;
    while(pre[r]!=r)
        r=pre[r];
    int i=x,j;
    while(i!=r)
    {
        j=pre[i];
        pre[i]=r;
        i=j;
    }
    return r;
}
void join(int x,int y)
{
    int a=find(x);
    int b=find(y);
    if(a!=b)
    {
        pre[a]=b;
    }
}
void into()
{
    for(int i=; i<N; i++)
    {
        pre[i]=i;
    }
}

int st[N][];

void init(int n)
{
    n++;
    for (int i = ; i < n; i++)
        st[i][] = x[i];

    for (int j = ; ( << j) <= n; j++)
    {
        for (int i = ; i + ( << j) -  < n; i++)
            st[i][j] = max(st[i][j - ],st[i + ( << (j - ))][j - ]);
    }
}

int search(int l, int r)
{
    int k = (int)(log((double)(r - l + )) / log(2.0));
    return max(st[l][k],st[r - ( << k) + ][k]);
}

int Ans;
void dfs(int i,int l,int r)
{
    int a=,b=;
    if(y[i]>l)
    {
        a=search(l,y[i]-);
        //cout<<i<<" "<<a<<endl;
        dfs(a,l,y[i]-);
    }
    if(y[i]<r)
    {
        b=search(y[i]+,r);
        //cout<<i<<" "<<b<<endl;
        dfs(b,y[i]+,r);
    }

    if(r-y[i]<y[i]-l)
    {
        for(int j=y[i]+; j<=r; j++)
        {
            if(find(i-x[j])==a)
            {
                Ans++;
            }
        }
    }
    else
    {
        for(int j=l; j<=y[i]-; j++)
        {
            if(find(i-x[j])==b)
            {
                Ans++;
            }
        }
    }
    if(a)
        join(a,i);
    if(b)
        join(b,i);
}

signed main()
{
    IOS;
    into();

    int n,a;
    cin>>n;

    for(int i=; i<=n; i++)
    {
        cin>>x[i];
        y[x[i]]=i;
    }

    init(n);

    dfs(n,,n);

    cout<<Ans;

    return ;
}