Digital Root 的推导

背景

在LeetCode上遇到这道题：Add Digits

大意是给一个数，把它各位数字相加得到一个数，如果这个数小于10就返回，不然继续 addDigits(这个相加得到的数)。

题目很简单，但是如果要用 O(1) 时间复杂度，不要涉及循环或递归来解答的话，我就不知道如何下手了。

于是我找了一下别人的解法，发现涉及到一个 Digital Root 的原理（由于维基百科打不开，所以我觉得有必要记录一下我搜集到的信息和理解）。

Digital Root

我是从这个网站上看到它的推导过程，但是为了防止以后这些引用的网站不存在或者访问不了，还是得自立更生写一下。

首先，A ≡ B mod C， ≡ 这个符号， 表示 A mod C 和 B mod C 得到的结果一样。（即 同余）

由于一个数的 digital sum 等于它所有位上的数加起来，即：

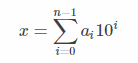
因为 10ⁱ ≡1ⁱ≡ 1 ( mod 9 )，所以：

推论出：一个数与它 各个位数和 的模9 同余。

从这个推论我们可以推导出：

f(f(x)) ≡ f(x) ≡ x (mod 9) (x=0 或 9 或 9的倍数 的情况除外）

为了同时兼顾 x=0 和 x=9 的情况，最后推导出来的公式是：

digital root = 1+ ((x-1) mod 9) 

（ps: 这么麻烦主要是为了兼顾 值为9的倍数 的数字）

（ps: 在计算机计算中，负数的模百家争鸣，所以最好把 0 的计算独立出来，免得为了 -1 % 9 伤脑筋）

延伸

同理可得，其他进制（非十进制）的数字的 digital root 也可以利用 同余 的原理推导出来，只不过 模的基数 以及 例外的情况 变了一下，例如如果计算八进制数字的 digital root，模的基数要取 7 而非 9，十六进制 则模的基数 为 15……

结论

1. digital root = 1+ ((x-1) mod 9)

2. 模运算真的能简化大数，好好利用可以省很多事。有空好好研究一下它的其他简化大数的功能。