SAP中MM模块基础数据之Quota Arrangement(配额协议)的解析
有的时候我们的采购部门有这样的需求, 同一颗物料有几个供应商同时供料, 这个时候就涉及到一个问题, 避免出现总是和一家供应商购买物料的情况,我们需求把这些物料按照一定的比列分配给供应商.在SAP系统中也为我们提供了这样的解决方案,大体上有两种解决方案
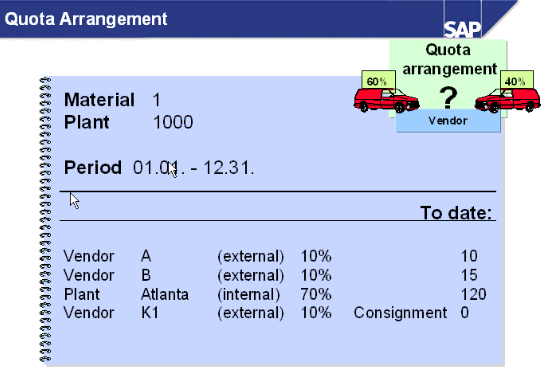
1,配合没有Split的Lot size的分配方案
本方案是和对供应商的供货没有明确的比例,只是为了避免总是像其中一家供应商购买物料,但是其他供应商总是要sample却从不购买的情况.

Allocation数量从开始做QA的分的数量开始计算,如果之前有给其中一家的数量可以通过放在quota base qty里 ,从下表中我们可以直观地看到不分割的逻辑计算。

2,配合有Split的Lot Size的分配方案 ,要使用QA需要前后台一起配合使用


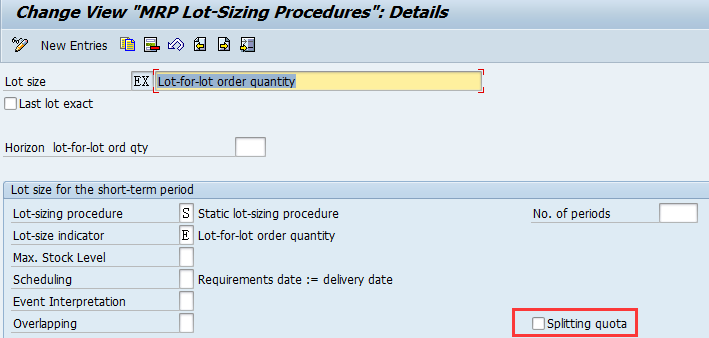

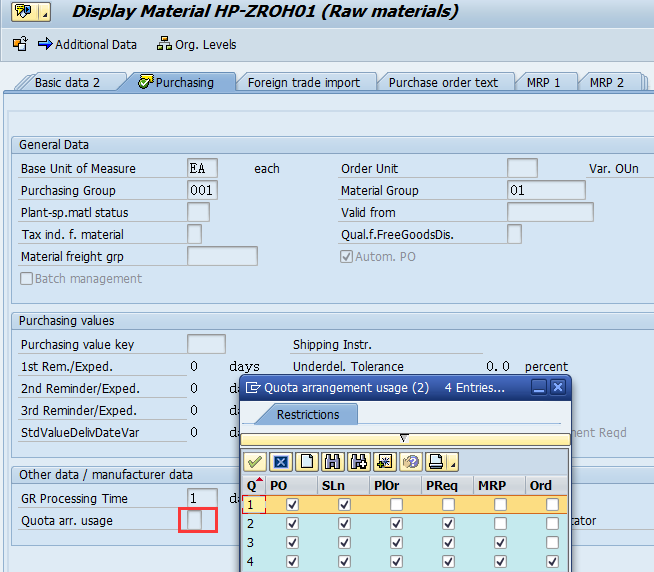
上图中1,2,3,4分别表示
1,表示会考虑PO和SA的数量参与已分配给供应商的数量的计算
2,表示会考虑PO,SA和计划订单的数量参与已分配给供应商的数量的计算
3,表示会考虑PO和SA,计划订单,PR,MRP的数量参与已分配给供应商的数量的计算
4,表示会考所有的数量参与已分配给供应商的数量的计算
SAP中MM模块基础数据之Quota Arrangement(配额协议)的解析的更多相关文章
- 【MM系列】SAP MM模块-基础配置第一篇
公众号:SAP Technical 本文作者:matinal 原文出处:http://www.cnblogs.com/SAPmatinal/ 原文链接:[MM系列]SAP MM模块-基础配置第一篇 ...
- SAP MM 模块常用的数据表
SAP MM模块常用数据表: Table Table Class Application Class Data Class Description EBAN TRANSP ME Transactio ...
- python中pandas数据分析基础3(数据索引、数据分组与分组运算、数据离散化、数据合并)
//2019.07.19/20 python中pandas数据分析基础(数据重塑与轴向转化.数据分组与分组运算.离散化处理.多数据文件合并操作) 3.1 数据重塑与轴向转换1.层次化索引使得一个轴上拥 ...
- 【MM系列】SAP MM模块-控制采购订单中某些项目的输出显示
公众号:SAP Technical 本文作者:matinal 原文出处:http://www.cnblogs.com/SAPmatinal/ 原文链接:[MM系列]SAP MM模块-控制采购订单中某些 ...
- 【MM系列】SAP 在SAP中更改基本计量单位
公众号:SAP Technical 本文作者:matinal 原文出处:http://www.cnblogs.com/SAPmatinal/ 原文链接:[MM系列]SAP 在SAP中更改基本计量单位 ...
- 【MM系列】SAP MM模块-组织结构介绍
公众号:SAP Technical 本文作者:matinal 原文出处:http://www.cnblogs.com/SAPmatinal/ 原文链接:[MM系列]SAP MM模块-组织结构介绍 ...
- Excel 将A表的基础数据拼接到B表中来-三种方法: ctrl+回车, VLOOKUP()函数,宏
A表 基础信息表 B表 业务信息表 将a表中的基础数据 拼接到B表的后面, 应用场景是: B表很多数据,很繁乱,名字不一定全, A表也是比较多的行,B表乱:比如有8行有李晨的,却只有3行是范仲淹的, ...
- 【MM系列】SAP MM模块-如何修改物料的移动平均价
公众号:SAP Technical 本文作者:matinal 原文出处:http://www.cnblogs.com/SAPmatinal/ 原文链接:[MM系列]SAP MM模块-如何修改物料的移动 ...
- 【MM系列】SAP MM模块-移动类型全部列表
公众号:SAP Technical 本文作者:matinal 原文出处:http://www.cnblogs.com/SAPmatinal/ 原文链接:[MM系列]SAP MM模块-移动类型全部列表 ...
随机推荐
- Java界面程序实现图片的放大缩小
Java界面程序实现图片的放大缩小.这个程序简单地实现了图片的打开.保存.放大一倍.缩小一倍和固定缩放尺寸,但是并没有过多的涵盖对图片的细节处理,只是简单地实现了图片大小的放缩. 思维导图如下: 效果 ...
- flask 之(三) --- 筛选|分页|过滤
筛选 查询数据筛选语法:类名.query.筛选符 .all( ):获取结果集:.count( ):获取查询到的对象数量 类名.query.filter(类名.属性.运算符('xxx')).all() ...
- 云计算Openstack介绍(1)
一.云计算的前世今生 所有的新事物都不是突然冒出来的,都有前世和今生.云计算也是IT技术不断发展的产物. 要理解云计算,需要对IT系统架构的发展过程有所认识. 请看下 IT系统架构的发展到目前为止大致 ...
- 【神经网络与深度学习】GLog使用笔记
环境: XPsp3 vs2005 glog-0.3.3 http://download.csdn.net/detail/chenguangxing3/6661667 编译: glog-0.3.3里面有 ...
- PHP 调用shell命令
可以使用的命令: popenfpassthrushell_execexecsystem 1.popen resource popen ( string command, string mode ) 打 ...
- ABC130 Task F. Minimum Bounding Box
题目链接 题解 最小的 bounding box 一定可以在四个时间段的最左端点和最右端点之间取到. 举例言之,设四个时间段分别是 (2, 5), (7, 10), (4, 9), ( 10, 20) ...
- thinkphp6下无法获取header头中的Authorization(apache版)
今天遇到在thinkphp框架中获取不到header头里边的 Authorization ,后来在.htaccess里面加多一项解决,记录下: <IfModule mod_rewrite.c&g ...
- Win32汇编-创建窗体代码
1.一个最简单的窗体的创建 ;>>>>>>>>>>>>>>>>>>>>>& ...
- Momentum Contrast for Unsupervised Visual Representation Learning
Momentum Contrast for Unsupervised Visual Representation Learning 一.Methods Previously Proposed 1. E ...
- Codeforces 1228C. Primes and Multiplication
传送门 当然是考虑 $n$ 的每个质数 $p$ 对答案的贡献 考虑 $p^k$ 在 $[1,m]$ 中出现了几次,显然是 $\left \lfloor \frac{m}{p^k} \right \rf ...
