指数家族-Beta分布

2. Beta分布

2.1 Beta分布

我们将由几个问题来得引出几个分布：

问题一：
1：  
2：把这个  个随机变量排序后得到顺序统计量  
3：问  是什么分布

首先我们尝试计算  落在一个区间  的概率，也就是如下概率值：

 
我们可以把  分成三段  。

我们考虑第一种情形：假设  个数中只有一个落在区间  内，则这个区间内的数  是第  大的，则  中应该有  个数，  中有  个数，我们将此描述为事件  ：

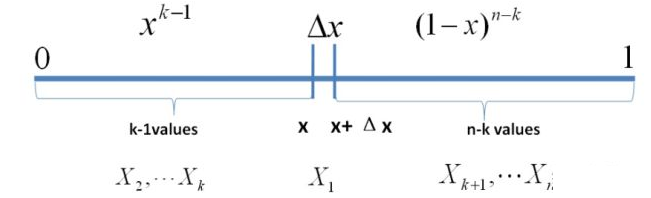
则有:

 
 是  的高阶无穷小。显然  个数落在  区间有  种取法，余下  个数中有  个数落在  中有  种组合，所以和事件  等价的事件一共有  个。

考虑第二种情形：假设  个数中只有两个落在区间  内：

 
则有:

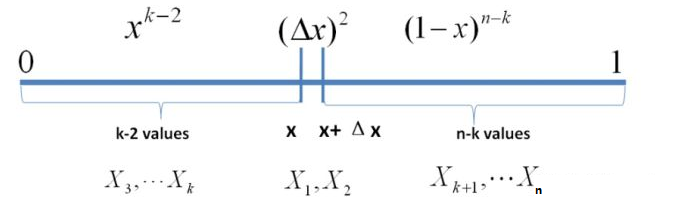
从以上分析可以得到：只要落在  内的数字超过一个，则对应的事件的概率就是  ，于是：

 
所以得到  的概率密度函数是：

 
我们知道利用Gamma函数可以把很多数学概念从整数集合延拓到实数集合。

我们在上式中取  ，于是得到：

 
这就是Beta分布了。

我们取Beta分布的峰值是胜率最大的。

2.2 可视化Beta分布

import numpy as np
from scipy.stats import beta
from matplotlib import pyplot as plt

alpha_values = [1/3,2/3,1,1,2,2,4,10,20]
beta_values = [1,2/3,3,1,1,6,4,30,20]
colors =  ['blue', 'orange', 'green', 'red', 'purple',
           'brown', 'pink', 'gray', 'olive']
x = np.linspace(0, 1, 1002)[1:-1]

fig, ax = plt.subplots(figsize=(14,9))

for a, b, c in zip(alpha_values, beta_values, colors):
    dist = beta(a, b)
    plt.plot(x, dist.pdf(x), c=c,label=r'$\alpha=%.1f,\ \beta=%.1f$' % (a, b))

plt.xlim(0, 1)
plt.ylim(0, 6)

plt.xlabel('$x$')
plt.ylabel(r'$p(x|\alpha,\beta)$')
plt.title('Beta Distribution')

ax.annotate('Beta(1/3,1)', xy=(0.014, 5), xytext=(0.04, 5.2),
            arrowprops=dict(facecolor='black', arrowstyle='-'))
ax.annotate('Beta(10,30)', xy=(0.276, 5), xytext=(0.3, 5.4),
            arrowprops=dict(facecolor='black', arrowstyle='-'))
ax.annotate('Beta(20,20)', xy=(0.5, 5), xytext=(0.52, 5.4),
            arrowprops=dict(facecolor='black', arrowstyle='-'))
ax.annotate('Beta(1,3)', xy=(0.06, 2.6), xytext=(0.07, 3.1),
            arrowprops=dict(facecolor='black', arrowstyle='-'))
ax.annotate('Beta(2,6)', xy=(0.256, 2.41), xytext=(0.2, 3.1),
            arrowprops=dict(facecolor='black', arrowstyle='-'))
ax.annotate('Beta(4,4)', xy=(0.53, 2.15), xytext=(0.45, 2.6),
            arrowprops=dict(facecolor='black', arrowstyle='-'))
ax.annotate('Beta(1,1)', xy=(0.8, 1), xytext=(0.7, 2),
            arrowprops=dict(facecolor='black', arrowstyle='-'))
ax.annotate('Beta(2,1)', xy=(0.9, 1.8), xytext=(0.75, 2.6),
            arrowprops=dict(facecolor='black', arrowstyle='-'))
ax.annotate('Beta(2/3,2/3)', xy=(0.99, 2.4), xytext=(0.86, 2.8),
            arrowprops=dict(facecolor='black', arrowstyle='-'))

plt.legend(loc=0)
plt.show()

从图中可以看出，Beta分布可以是凹的、凸的、单调上升的、单调下降的；可以是曲线也可以是直线，而均匀分布也特殊的Beta分布。可以尝试改下参数，看看Beta分布的各种形态。

2.3 Beta-Binomial共轭

问题二：
1：  ，排序后对应的顺序统计量  ，我们要猜测  ；
2：  中有  个比  小，  个比  大；
3：问  是什么分布

由于  在  中是第  大的，我们容易推得到  在  这  个独立随机变量中是第  大的。可以按上一节的推导，此时  的概率密度是  。

按贝叶斯推导的逻辑：
1)：  是我们要猜测的参数，我们推导出  的分布是  ，称为  的先验分布。
2)：数据  中有  个比  小，  个比  大，  相当于做了  次贝努力实验，所以  服从二项分布  。
3)：在给定来自数据的提供的  知识后，  的后验分布为 

贝叶斯参数估计的基本过程是：

先验分布+数据知识=后验分布

因此可以得到：

更一般的，对于非负实数  ，我们有如下关系：

以上式子实际上描述的就是Beta-Binomial共轭。共轭意思是先验和后验都服从同一个分布形式。这种形式不变，我们能够在先验分布中赋予参数很明确的物理意义，这个物理意义可以延伸到后验分布中进行解释，同时从先验变换到后验的过程中从数据中补充的知识也容易有物理解释。（我感觉有共轭后计算更容易哈，因为形式都知道了，其他的就是凑参数了。还有另一个好处是:每当有新的观测数据，就把上次的后验概率作为先验概率，乘以新数据的likelihood，然后就得到新的后验概率，而不必用先验概率乘以所有数据的likelihood得到后验概率。）

从前面的过程中可以知道，Beta分布中的参数  也可以理解为物理计数，这两个参数经常被称为伪计数(pseudo-count)。基于以上逻辑，我们可以把  写成下式来理解：

 
其中  恰好的均匀分布  。

对于上式，可以从贝叶斯角度来理解。假设有一个不均匀的硬币抛出正面的概率是  ，抛  次后得到正面和反面的次数分别为  次，那按传统概率学派的观点，  的估计是  。而从贝叶斯学派的角度来看，开始对硬币的不均匀性一无所知，所以假设  ，于是有了二项分布的计数  后，按照贝叶斯的公式计算  的后验分布：

 
计算得到后验分布为正好是： 

前面从二项分布推导Gamma分布的时候，使用了如下等式：
 
左边是二项分布的概率累积，右边是  分布的概率累积。现在我们来证明这个等式。

我们构造如下二项分布，取随机变量  ，一个成功的贝努力实验就是 

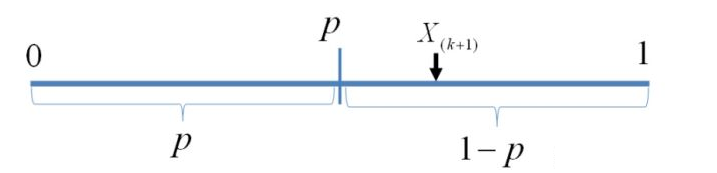
我们可以得到：
 
此处  是顺序统计量，为第  大的数。上述等式意思是：成功至多  次等于第  大的数必定失败（即失败至少  次）。由于  ，于是

2.4 Beta分布的应用

1. 棒球击球率

那么我们简单说个Beta-Binomial共轭的应用。用一句话来说，beta分布可以看作一个概率的概率分布，当你不知道一个东西的具体概率是多少时，它可以给出了所有概率出现的可能性大小。

举一个简单的例子，熟悉棒球运动的都知道有一个指标就是棒球击球率(batting average)，就是用一个运动员击中的球数除以击球的总数，我们一般认为0.266是正常水平的击球率，而如果击球率高达0.3就被认为是非常优秀的。现在有一个棒球运动员，我们希望能够预测他在这一赛季中的棒球击球率是多少。传统的频率学派会直接计算棒球击球率，用击中的数除以击球数，但是如果这个棒球运动员只打了一次，而且还命中了，那么他就击球率就是100%了，这显然是不合理的，因为根据棒球的历史信息，我们知道这个击球率应该是0.215到0.36之间才对。对于这个问题，我们可以用一个二项分布表示（一系列成功或失败），一个最好的方法来表示这些经验（在统计中称为先验信息）就是用beta分布，这表示在我们没有看到这个运动员打球之前，我们就有了一个大概的范围。beta分布的定义域是  这就跟概率的范围是一样的。接下来我们将这些先验信息转换为beta分布的参数，我们知道一个击球率应该是平均0.27左右，而他的范围是0.21到0.35，那么根据这个信息，我们可以取  。（这样取值可以从Beta的均值和分布考虑）