[CSP-S模拟测试]:y（DP+bitset）

题目背景

$\frac{1}{4}$遇到了一道水题，叕完全不会做，于是去请教小$D$。小$D$懒得理$\frac{1}{4}$，直接就离开了。于是，$\frac{1}{4}$只好来问你，这道题是这样的：

---

题目描述

给定一个无向图，$n$个点（从$1$开始编号）、$m$条边（长度为$1$），每条边有一个权值$c(c\in\{0，1\})$。
一条路径，可以表示为一个长度为经过边数的$01$串，串的第$i$位为经过的第$i$条边的权值。
两条路径相同，当且仅当表示其的$01$串相同。
求从$1$号点出发、长度为$d$的路径种数。

---

输入格式

从文件$y.in$中读入数据。
第一行，三个整数，$n,m,d$。
接下来$m$行，每行三个整数$u,v,c$，代表一条边连接$u$和$v$，权值为$c$。

---

输出格式

输出到文件$y.out$中。
输出一行，一个整数，代表答案。

---

样例

样例输入：

3 2 3
1 2 0
1 3 1

样例输出：

4

---

数据范围与提示

样例解释：

$1\rightarrow 2\rightarrow 1\rightarrow 2\Rightarrow 000$
$1\rightarrow 2\rightarrow 1\rightarrow 3\Rightarrow 001$
$1\rightarrow 3\rightarrow 1\rightarrow 2\Rightarrow 110$
$1\rightarrow 3\rightarrow 1\rightarrow 3\Rightarrow 111$

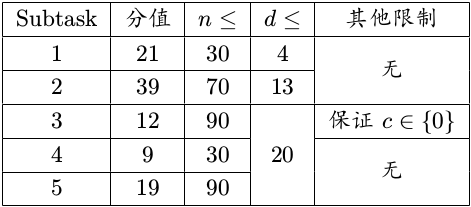
数据范围：

保证$n\in [1,90],m\in [0,n\times (n−1)],d\in [1,20],u,v\in [1,n],c\in\{0,1\}$。

---

题解

考虑$DP$，设$dp[i][j][stack]$表示从$i$到$j$是否有一条状态为$stack$的连边。

那么显然时间复杂度是：$\Theta(s^d\times n\times (n+m))$的。

考虑第一个优化，使用$bitset$，我们能够优化掉$j$那一维。

但是时间复杂度还是不够，于是我们考虑$meet\ in\ the\ middle$算法，只算前一半即可。

时间复杂度：$\Theta(2^{\frac{d}{2}}\times n\times (n+m)+2^d\times n)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
int n,m,d;
bitset<90> bit[4][1100000];
long long ans;
int main()
{
	scanf("%d%d%d",&n,&m,&d);
	for(int i=1;i<=m;i++)
	{
		int u,v,c;
		scanf("%d%d%d",&u,&v,&c);
		if(c)bit[1][u][v]=bit[1][v][u]=1;
		else bit[0][u][v]=bit[0][v][u]=1;
	}
	int dis=(d+1)>>1;
	for(int i=n;i;i--)
	{
		for(int j=0;j<(1<<d);j++)bit[2][j].reset();
		bit[2][1][i]=1;
		for(int j=1;j<(1<<dis);j++)
			for(int k=1;k<=n;k++)
			{
				if(!bit[2][j][k])continue;
				bit[2][j<<1]|=bit[0][k];
				bit[2][j<<1|1]|=bit[1][k];
			}
		for(int j=0;j<(1<<dis);j++)
			bit[3][j][i]=bit[2][(1<<dis)|j].count()?1:0;
	}
	for(int i=0;i<(1<<dis);i++)
		for(int j=0;j<(1<<(d-dis));j++)
			if(((bit[3][i]&bit[2][(1<<(d-dis))|j]).count()))ans++;
	printf("%lld",ans);
	return 0;
}

---

rp++