决策树剪枝算法-悲观剪枝算法(PEP)

前言

　　在机器学习经典算法中，决策树算法的重要性想必大家都是知道的。不管是ID3算法还是比如C4.5算法等等，都面临一个问题，就是通过直接生成的完全决策树对于训练样本来说是“过度拟合”的，说白了是太精确了。由于完全决策树对训练样本的特征描述得“过于精确” ,无法实现对新样本的合理分析, 所以此时它不是一棵分析新数据的最佳决策树。解决这个问题的方法就是对决策树进行剪枝，剪去影响预测精度的分支。常见的剪枝策略有预剪枝(pre -pruning)技术和后剪枝(post -pruning )技术两种。预剪枝技术主要是通过建立某些规则限制决策树的充分生长, 后剪枝技术则是待决策树充分生长完毕后再进行剪枝。由于预剪枝技术运用较少，本系列将着重介绍后剪枝技术，本文将介绍的是悲观剪枝技术。

一、统计学相关知识复习

　　1、置信区间：

　　　　设θ'在大样本下服从E(θ') = θ, 标准误差为σ'的正态分布，那么θ的(1 - α)100%置信区间是：

　　　　　　θ' +/- (Zα/2) σ'

　　2、二项式概率分布：

　　　均值和方差分别是u = np, σ2=npq　,其中p=每次实验成功的概率， q=1-p。

　　3、二项分布的正态逼近

　　　　如果np>=4 且nq>=4 ,二项概率分布p(y)逼近于正态分布。如下图

　　

　　可以看到P(Y<=2)是在正态曲线下Y=2.5的左端面积。注意到Y=2的左端面积是不合适的，因为它省略了相应于Y=2的一半概率的长方形。为了修正，用连续概率分布去近似离散概率分布，在计算概率之前我们需要将2增加0.5。值0.5称为二项概率分布近似的连续性修正因子，因此

P(Y<=a) 约等于 P(Z<  (a+0.5 - np/ ( npq)1/2)   )；

P(Y>=a) 约等于 P(Z> (a-0.5 - np/ ( npq)1/2)   )

　　

二、剪枝过程

　　对于后剪枝技术，在决策树形成后，最先要做的就是剪枝。后剪枝的剪枝过程是删除一些子树，然后用其叶子节点代替，这个叶子节点所标识的类别通过大多数原则(majority class criterion)确定。所谓大多数原则，是指剪枝过程中, 将一些子树删除而用叶节点代替,这个叶节点所标识的类别用这棵子树中大多数训练样本所属的类别来标识,所标识的类称为majority class ，（majority class 在很多英文文献中也多次出现）。

三、悲观剪枝--Pessimistic Error Pruning (PEP)

　　PEP后剪枝技术是由大师Quinlan提出的。它不需要像REP(错误率降低修剪)样，需要用部分样本作为测试数据，而是完全使用训练数据来生成决策树，又用这些训练数据来完成剪枝。决策树生成和剪枝都使用训练集, 所以会产生错分。现在我们先来介绍几个定义。

　　T1为决策树T的所有内部节点(非叶子节点)，

　　T2为决策树T的所有叶子节点，

　　T3为T的所有节点，有T3=T1∪T2,

　　n(t)为t的所有样本数,

　　ni(t)为t中类别i的所有样本数，

　　e(t)为t中不属于节点t所标识类别的样本数

　　在剪枝时，我们使用

　　　　r(t)=e(t)/n(t)

　　就是当节点被剪枝后在训练集上的错误率，而

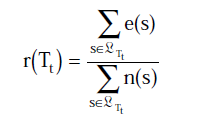　　, 其中s为t节点的叶子节点。

　　在此，我们把错误分布看成是二项式分布，由上面“二项分布的正态逼近”相关介绍知道，上面的式子是有偏差的，因此需要连续性修正因子来矫正数据，有

　　r‘(t)=[e(t) + 1/2]/n(t)

　　和

　　, 其中s为t节点的叶子节点，你不认识的那个符号为 t的所有叶子节点的数目

　　为了简单，我们就只使用错误数目而不是错误率了，如下

　　e'(t) = [e(t) + 1/2]

　　

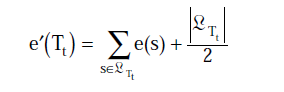
　　接着求e'(Tt)的标准差，由于误差近似看成是二项式分布，根据u = np, σ2=npq可以得到

　　

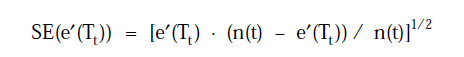
　　当节点t满足

　　

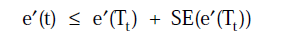
　　则Tt就会被裁减掉。

　　

四、总结

　　在学习机器学习中，由于涉及的知识比较多，面又很广，所以大家一定要把数学，统计学，算法等相关知识学透彻，多总结归纳。而且这些知识一般比较晦涩难懂，但看别人的博客往往由于他人对知识点的理解有误，而导致对读者本人的误导，且博客是不具权威，不保证正确的，所以对机器学习这种严谨的学科更是需要多参考，多阅读特别是文献，甚至是算法原著者的论文。同时对我理解有误的地方，欢迎大家指出，再次表示感谢了。

五、推荐阅读

　　 想了解其他剪枝算法(REP, MEP, EBP)的可以参考这篇文章http://52weis.com/articles.html?id=718_21

六、参考文献

　　A Comparative Analysis of Methods for Pruning Decision Trees 1997（ISSUE）

　　决策树的剪枝理论　

　　决策树理论

　　C4.5决策树

　　THE EFFECTS OF PRUNING METHODS ON THE PREDICTIVE ACCURACY OF INDUCED（ISSUE）

　　决策树后剪枝算法的研究  范　洁　杨岳湘（ISSUE）

　　决策树剪枝方法的比较 魏红宁 2005（ISSUE）

　　悲观剪枝算法在学生成绩决策树中的应用 李萍 2014（ISSUE）

　　

　　　

每篇技术博客，应该像代码一样，条理清晰，易于阅读，同时又应该简洁，观点鲜明，这才是一篇合格的技术博客。（一切为了知识的传播）。文章首发www.52weis.com
所有文章均系原创，转载请注明作者和本文链接