LG_3457_[POI2007]POW-The Flood

题目描述

Description 你手头有一张该市的地图。这张地图是边长为 m∗n 的矩形,被划分为m∗n个1∗1的小正方形。对于每个小正方形,地图上已经标注了它的海拔高度以及它是否是该市的一个组成部分。地图上的所有部分都被水淹没了。并且,由于这张地图描绘的地面周围都被高山所环绕,洪水不可能自动向外排出。显然,我们没有必要抽干那些非该市的区域。

每个巨型抽水机可以被放在任何一个1∗1正方形上。这些巨型抽水机将持续地抽水直到这个正方形区域里的水被彻底抽干为止。当然,由连通器原理,所有能向这个格子溢水的格子要么被抽干,要么水位被降低。每个格子能够向相邻的格子溢水,“相邻的”是指(在同一高度水平面上的射影)有公共边。

Input

第一行是两个数m,n(1<=m,n<=1000).

以下 m 行,每行 n 个数,其绝对值表示相应格子的海拔高度;若该数为正,表示它是该市的一个区域;否则就不是。

请大家注意:所有格子的海拔高度其绝对值不超过 1000 ,且可以为零.

Output

只有一行,包含一个整数,表示至少需要放置的巨型抽水机数目。

感谢@FlashHu 提供的翻译

样例

INPUT

6 9

-2 -2 -1 -1 -2 -2 -2 -12 -3

-2 1 -1 2 -8 -12 2 -12 -12

-5 3 1 1 -12 4 -6 2 -2

-5 -2 -2 2 -12 -3 4 -3 -1

-5 -6 -2 2 -12 5 6 2 -1

-4 -8 -8 -10 -12 -8 -6 -6 -4

OUTPUT

2

HINT

SOLUTION

并查集维护连通块。

其实对于题面的“连通器”原理，考场上并没有理解，导致根本看不懂样例。

其实这个模型相信大家一定见过，只是我在场上完全没有想起来。



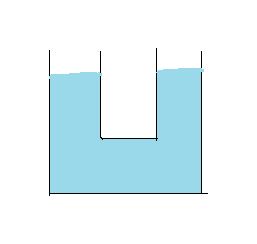
很明显地，当右边的水位因为某种原因下降时，左边的会一同下降。

而且当i,j相邻，\(h_i\leq h_j\)时，若i点水被抽尽，j点一定也被抽尽。

所以根据这些原理，设我们的抽水机的高度为\(h_i\)，那么只要相邻的点满足\(h_j\leq h_i\)即可把i,j合并。

显然本题是要我们维护连通块，考虑使用bfs或并查集实现。

我们这里使用的是并查集，枚举点向四周扩散合并。

为了方便枚举相同高度的点，我们考虑把所有点按高度升序排序。

当我们的高度相同的点枚举完，要进行一次统一合并之后再统计答案。

栗子：

数据：

1 4

3 3 -2 1

在枚举高度为3的点（左）之前，现在已有的连通块情况：

（3）（3）（2 1）

若我们在枚举完左边的3之后直接统计的话会出现情况：

（3 3）（2 1）

答案凭空多了1

因为我们做的不是bfs所以并不能像bfs那样扩散的十分彻底。这个操作就可以避免出现“连通不彻底”的情况。

本题的思维难度较高。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <map>
using namespace std;
inline int read(){
	int x=0,f=1;char ch=getchar();
	while (ch<'0'||ch>'9') {if (ch=='-') f=-1;ch=getchar();}
	while (ch>='0'&&ch<='9') {x=x*10+ch-48;ch=getchar();}
	return x*f;}
const int N=1010;
const int dx[4]={-1,1,0,0},dy[4]={0,0,-1,1};
int n,m,sq[N][N],fa[N*N],cnt=0;
bool used[N*N];
struct NODE{int x,y,h;}q[N*N];
struct NODE2{int x,y;}nd[N*N];
inline int find (int x) {return (x==fa[x])?x:fa[x]=find(fa[x]);}
bool cmp(NODE a,NODE b){return a.h<b.h;}
int main(){
	int i,j;
	n=read();m=read();int ans=0;
	for (i=1;i<=n;++i) for (j=1;j<=m;++j){
		sq[i][j]=read();fa[++cnt]=cnt;
		q[cnt].x=i;q[cnt].y=j;q[cnt].h=abs(sq[i][j]);}
	sort(q+1,q+1+cnt,cmp);memset(used,0,sizeof(used));
	for (i=1;i<=cnt;++i){
		int x=q[i].x,y=q[i].y;
		int frm=(x-1)*m+y;
		for (j=0;j<4;++j){
			int nx=x+dx[j],ny=y+dy[j];
		//	puts("******");
			if ((nx<1)||(ny<1)||(nx>n)||(ny>m)) continue;
			if (abs(sq[x][y])<abs(sq[nx][ny])) continue;
		//	printf("(%d,%d):%d,%d\n",x,y,nx,ny);
			int now=(nx-1)*m+ny;
			int f1=find(frm),f2=find(now);
			if (f2==f1) continue;
			fa[f2]=f1;used[f1]|=used[f2];
		}
		if (q[i].h!=q[i+1].h){
			for (j=i;(q[i].h==q[j].h);--j){
				int x=find((q[j].x-1)*m+q[j].y);
				if (sq[q[j].x][q[j].y]<=0) continue;
				if (!used[x]) {used[x]=1;ans++;}
			}
		}
	}
	printf("%d\n",ans);
	return 0;
}