luogu P2762 太空飞行计划问题

好像是最大权闭合图，也就是最大流最小割啦，找出最大流的路径输出，这题如何建模呢，一样的先设源点和汇点，源点向每个计划连capacity为赞助数的边，每个计划连相应装置capacity为无穷的边，每个装置向汇点连capacity为支付费用的边，这样，最大利润就是赞助总数-最大流啦，如何证？看两个例子

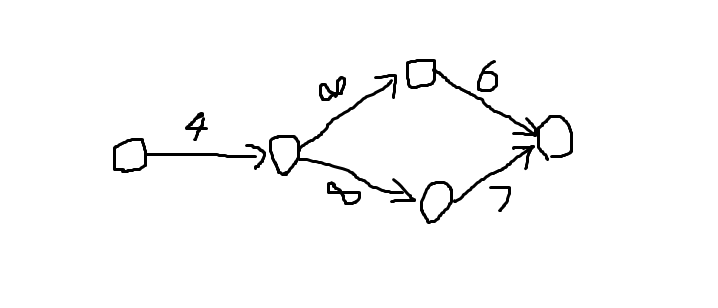
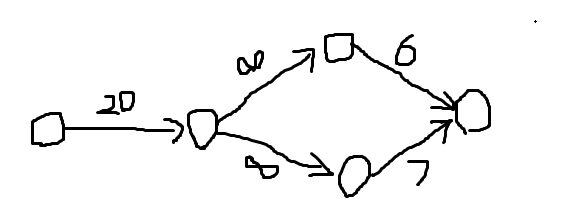
若是可行方案，相减即为利润，若是不可行方案，相减就为0，数学归纳法可推知n个时也对

另一个问题，如何找到最大权闭合图呢，最后一次分层的level数组就可以帮忙了，我们知道退出dinic算法就是无法到达汇点，考虑如何分层，满足两个条件，capacity大于flow且尚未分层，我们知道，对答案有贡献的是到计划的那条边的capacity比其相应的装置的capacity加起来还要大，最后一次分层时，即已经达到最大流，若从源点到某个计划无法分层，说明其capacity<=对应装置的，那就一定不选，能分层的一定是源有余而汇不进，又计划和装置之间的流量是无穷，则一定可以分层，直接考虑最后一层的level数组并输出即可，附上别个大佬的解释(

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) ((x)&(-x))
typedef long long LL;

const int maxm = 1e4+;
const int INF = 0x3f3f3f3f;

struct edge{
    int u, v, cap, flow, nex;
} edges[maxm];

int head[maxm], cur[maxm<<], cnt, level[], give[], cost[];
vector<int> req[];

void init() {
    memset(head, -, sizeof(head));
}

void add(int u, int v, int cap) {
    edges[cnt] = edge{u, v, cap, , head[u]};
    head[u] = cnt++;
}

void addedge(int u, int v, int cap) {
    add(u, v, cap), add(v, u, );
}

void bfs(int s) {
    memset(level, -, sizeof(level));
    queue<int> q;
    level[s] = ;
    q.push(s);
    while(!q.empty()) {
        int u = q.front();
        q.pop();
        for(int i = head[u]; i != -; i = edges[i].nex) {
            edge& now = edges[i];
            if(now.cap > now.flow && level[now.v] < ) {
                level[now.v] = level[u] + ;
                q.push(now.v);
            }
        }
    }
}

int dfs(int u, int t, int f) {
    if(u == t) return f;
    for(int& i = cur[u]; i != -; i = edges[i].nex) {
        edge& now = edges[i];
        if(now.cap > now.flow && level[u] < level[now.v]) {
            int d = dfs(now.v, t, min(f, now.cap - now.flow));
            if(d > ) {
                now.flow += d;
                edges[i^].flow -= d;
                return d;
            }

        }
    }
    return ;
}

int dinic(int s, int t) {
    int maxflow = ;
    for(;;) {
        bfs(s);
        if(level[t] < ) break;
        memcpy(cur, head, sizeof(head));
        int f;
        while((f = dfs(s, t, INF)) > )
            maxflow += f;
    }
    return maxflow;
}

void run_case() {
    init();
    int n, m;
    scanf("%d%d", &m, &n);
    char in[];
    int s = , t = m++n, sum = ;
    for(int i = ; i <= m; ++i) {
        scanf("%d", &give[i]);
        sum += give[i];
        memset(in, , sizeof(in));
        cin.getline(in, );
        int ulen = , num;
        while(sscanf(in+ulen, "%d", &num) == ) {
            req[i].push_back(num);
            if(num == ) ulen++;
            else while(num) {
                num /= ; ulen++;
            }
            ulen++;
        }
    }
    for(int i = ; i <= n; ++i)
        scanf("%d", &cost[i]);
    for(int i = ; i <= m; ++i) {
        addedge(s, i, give[i]);
        for(int j = ; j < req[i].size(); ++j)
            addedge(i, m+req[i][j], INF);
    }
    for(int i = ; i <= n; ++i)
        addedge(i+m, t, cost[i]);
    int ans = sum - dinic(s, t);
    for(int i = ; i <= m; ++i) {
        if(level[i] != -) printf("%d ", i);
    }
    printf("\n");
    for(int i = ; i <= n; ++i)
        if(level[i+m] != -) printf("%d ", i);
    printf("\n%d", ans);
}

int main() {
    ios::sync_with_stdio(false), cin.tie();
    run_case();
    //cout.flush();
    return ;
}