Largest Allowed Area【模拟+二分】

Largest Allowed Area

题目链接（点击）

题目描述

A company is looking for land to build its headquarters. It has a lot of money and can buy as many land patches as it needs. Its goal, however, is finding the largest square region containing no forest. Unfortunately, there is no such region that is large enough for the headquarters they want to build. 

   

After negotiation with the government and the evaluation of environmental impacts, the government allows the company to purchase land with at most one forest patch. In other words, the company’s goal is now finding the largest square region containing at most one forest patch. 

 

To facilitate the search process, the company creates a map in the form of a 2D table consisting R rows and C columns. In this 2D table, each entry represents a land of patch where 0 corresponds to a non-forest patch and 1 to a forest patch. Unfortunately, the map may have up to 1,000 x 1,000 entries and it is not a good idea to manually look for the largest allowed square region. This is where your skill comes into play. Write an efficient algorithm to find such a square region.

输入

The first line is a positive integer T <= 20 representing the number of test cases. For each case, the input is formatted as follows.

Note: there is at least one non-forest patch in each test case.

样例输入

2
10 20
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
20 10
1 0 0 0 0 1 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 1 0
0 0 1 0 0 0 0 1 1 0
0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 1 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 1 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 0 0

样例输出

9
7

输出

There are T lines in the output. Each line is the number of rows in the largest allowed square region for each case.

题意：

给出n*m的矩阵 其中只包含0和1 要求在里面找出 边长最大的正方形 最多可以使用1个1

思路：

学长的思路 感觉很好

首先根据输入打好一张表：任意坐标位置 其左上部分包含该点上方和左方 全部点 1的总个数

例如示例1 打好表如下：

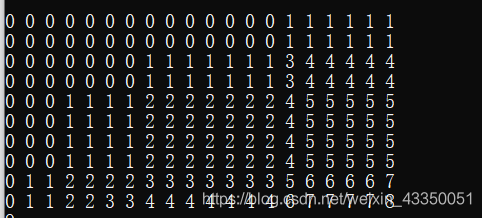
先枚举出 目标矩阵的边长 1 ~ min (n,m)

然后再用两层for循环 枚举x和y表示 矩阵左上角放置的位置 如果符合条件（即正方形内部1的个数<=1即可）直接跳出循环

因为枚举的边长是从大到小的 所以首先找到的一定是符合条件即最大的 代码如下：但T了

#include<bits/stdc++.h>
using namespace std;
const int MAX=1e3;
int a[MAX+5][MAX+5],b[MAX+5][MAX+5];
int main()
{
    int T;
    scanf("%d",&T);
    while(T--){
        int n,m;
        scanf("%d%d",&n,&m);
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                scanf("%d",&a[i][j]);
                b[i][j]=b[i][j-1]+b[i-1][j]-b[i-1][j-1]+a[i][j];
            }
        }
        /*
        printf("\n\n");
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                printf("%d ",b[i][j]);
            }
            printf("\n");
        }
        */
        int flag=0,flag1=0,ans=0;
        for(int k=min(n,m);k>=0;k--){
            //printf("%d ",k);
            for(int i=0;i+k<n;i++){
                for(int j=0;j+k<m;j++){
                    if(b[i][j]+b[i+k-1][j+k-1]-b[i-1][j+k-1]-b[i+k-1][j-1]<=1){
                        ans=k;
                        flag=1;
                        break;
                    }
                }
                if(flag==1){
                    flag1=1;
                    break;
                }
            }
            if(flag1==1){
                break;
            }
        }
        printf("%d\n",ans);
    }
    return 0;
}

优化：

通过二分枚举的正方形边长方法降低复杂度 因为 当mid符合条件的时候 mid+1 ~ min(n,m)  也可能符合条件 反之 1 ~ mid-1 也可能是符合条件的

AC代码：

#include<bits/stdc++.h>
using namespace std;
const int MAX=1e3;
int a[MAX+5][MAX+5],b[MAX+5][MAX+5];
int main()
{
    int T;
    scanf("%d",&T);
    while(T--){
        int n,m;
        scanf("%d%d",&n,&m);
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                scanf("%d",&a[i][j]);
                b[i][j]=b[i][j-1]+b[i-1][j]-b[i-1][j-1]+a[i][j];
            }
        }
        int ans=0;
        if(b[n-1][m-1]!=n*m){
            int l=0,r=min(n-1,m-1);
            while(l<=r){
                int k=(l+r)/2,flag=0,flag1=0;
                for(int i=0;i+k-1<n;i++){
                    for(int j=0;j+k-1<m;j++){
                        if(b[i-1][j-1]+b[i+k-1][j+k-1]-b[i-1][j+k-1]-b[i+k-1][j-1]<=1){
                            ans=k;
                            flag=1;
                            break;
                        }
                    }
                    if(flag==1){
                        flag1=1;
                        break;
                    }
                }
                if(flag1==1){
                    l=k+1;
                }
                else{
                    r=k-1;
                }
            }
        }
        printf("%d\n",ans);
    }
    return 0;
}