【Codeforces Round】 #431 (Div. 2) 题解

Codeforces Round #431 (Div. 2) 

A. Odds and Ends

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Where do odds begin, and where do they end? Where does hope emerge, and will they ever break?

Given an integer sequence a1, a2, ..., an of length n. Decide whether it is possible to divide it into an odd number of non-empty subsegments, the each of which has an odd length and begins and ends with odd numbers.

A subsegment is a contiguous slice of the whole sequence. For example, {3, 4, 5} and {1} are subsegments of sequence {1, 2, 3, 4, 5, 6}, while {1, 2, 4} and {7} are not.

Input

The first line of input contains a non-negative integer n (1 ≤ n ≤ 100) — the length of the sequence.

The second line contains n space-separated non-negative integers a1, a2, ..., an (0 ≤ ai ≤ 100) — the elements of the sequence.

Output

Output "Yes" if it's possible to fulfill the requirements, and "No" otherwise.

You can output each letter in any case (upper or lower).

Examples

　　input

3
1 3 5

　　output

Yes

　　input

5
1 0 1 5 1

　　output

Yes

　　input

3
4 3 1

　　output

No

　　input

4
3 9 9 3

　　output

No

Note

In the first example, divide the sequence into 1 subsegment: {1, 3, 5} and the requirements will be met.

In the second example, divide the sequence into 3 subsegments: {1, 0, 1}, {5}, {1}.

In the third example, one of the subsegments must start with 4 which is an even number, thus the requirements cannot be met.

In the fourth example, the sequence can be divided into 2 subsegments: {3, 9, 9}, {3}, but this is not a valid solution because 2 is an even number.

题目大意：给一个序列，要求分成奇数个首位都是奇数且长度为奇数的序列

试题分析：(官方题解) div-2第一题不要想复杂，因为偶数个奇数为偶数，奇数个奇数为奇数的原则，所以只需判断首位是否是奇数且长度为奇数即可。

　　　　　(我的题解)想复杂了，dp[i][0]表示前i个已经分配完了(包括i)，分了偶数段

　　　　　　　　　　　　　　　　　　　　　　　  dp[i][1]表示前i个已经分配完了(包括i)，分了奇数段

　　　　　　　　　 转移就是 dp[i][0]=1 (dp[i-j][1]==true&&a[i-j+1]%2==1&&j%2==1)

　　　　　　　　　　　　　  dp[i][1]=1 (dp[i-j][0]==true&&a[i-j+1]%2==1&&j%2==1)

代码：

#include<iostream>
#include<cstring>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;

#define LL long long

inline int read(){
	int x=0,f=1;char c=getchar();
	for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
	for(;isdigit(c);c=getchar()) x=x*10+c-'0';
	return x*f;
}
const int INF=9999999;
const int MAXN=100000;
int N; int a[MAXN+1];
bool dp[MAXN+1][2];

int main(){
	N=read();
	for(int i=1;i<=N;i++){
		a[i]=read();
	}
	dp[0][0]=true;
	for(int i=1;i<=N;i++){
		if(a[i]%2==0) continue;
		for(int j=1;j<=i;j+=2)
			if(a[i-j+1]%2!=0&&dp[i-j][0]) {dp[i][1]=true;break;}
		for(int j=1;j<=i;j+=2)
			if(a[i-j+1]%2!=0&&dp[i-j][1]) {dp[i][0]=true;break;}
	}
	if(dp[N][1]){puts("Yes");}
	else puts("No");
	return 0;
}

　

B. Tell Your World

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Connect the countless points with lines, till we reach the faraway yonder.

There are n points on a coordinate plane, the i-th of which being (i, yi).

Determine whether it's possible to draw two parallel and non-overlapping lines, such that every point in the set lies on exactly one of them, and each of them passes through at least one point in the set.

Input

The first line of input contains a positive integer n (3 ≤ n ≤ 1 000) — the number of points.

The second line contains n space-separated integers y1, y2, ..., yn ( - 109 ≤ yi ≤ 109) — the vertical coordinates of each point.

Output

Output "Yes" (without quotes) if it's possible to fulfill the requirements, and "No" otherwise.

You can print each letter in any case (upper or lower).

Examples

　　input

5
7 5 8 6 9

　　output

Yes

　　input

5
-1 -2 0 0 -5

　　output

No

　　input

5
5 4 3 2 1

　　output

No

　　input

5
1000000000 0 0 0 0

　　output

Yes

Note

In the first example, there are five points: (1, 7), (2, 5), (3, 8), (4, 6) and (5, 9). It's possible to draw a line that passes through points 1, 3, 5, and another one that passes through points 2, 4 and is parallel to the first one.

In the second example, while it's possible to draw two lines that cover all points, they cannot be made parallel.

In the third example, it's impossible to satisfy both requirements at the same time.

题目大意：有N个点，每个点坐标为(i,yi)，要求用两条且必用两条平行线穿过所有点，问是否可行。

试题分析：因为一开始理解错了题意，所以最后一直顺着复杂的思路写了QAQ

　　　　　其实可以想到，只需要枚举两个点，其y差值作为斜率，然后看是否可行就可以了。

代码：

#include<iostream>
#include<cstring>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;

#define LL long long

inline int read(){
	int x=0,f=1;char c=getchar();
	for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
	for(;isdigit(c);c=getchar()) x=x*10+c-'0';
	return x*f;
}
const int INF=9999999;
const int MAXN=100000;

int N;
int a[MAXN+1];
bool judge(double dis){
	int fir=-1;
	for(int i=2;i<=N;i++){
		if((i-1)*dis==a[i]-a[1]) continue;
		if(fir==-1) fir=i;
		else if((i-fir)*dis!=a[i]-a[fir]) return false;
	}
	if(fir!=-1) return true;
    return false;
} 

int main(){
	N=read();
	for(int i=1;i<=N;i++) a[i]=read();
	if(judge(a[2]-a[1])||judge((a[3]-a[1])/2.0)||judge(a[3]-a[2])){
		puts("Yes"); return 0;
	}
	puts("No");
	return 0;
}

 

C. From Y to Y

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

From beginning till end, this message has been waiting to be conveyed.

For a given unordered multiset of n lowercase English letters ("multi" means that a letter may appear more than once), we treat all letters as strings of length 1, and repeat the following operation n - 1 times:

• Remove any two elements s and t from the set, and add their concatenation s + t to the set.

The cost of such operation is defined to be 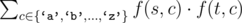, where f(s, c) denotes the number of times character c appears in string s.

Given a non-negative integer k, construct any valid non-empty set of no more than 100 000 letters, such that the minimum accumulative cost of the whole process is exactly k. It can be shown that a solution always exists.

Input

The first and only line of input contains a non-negative integer k (0 ≤ k ≤ 100 000) — the required minimum cost.

Output

Output a non-empty string of no more than 100 000 lowercase English letters — any multiset satisfying the requirements, concatenated to be a string.

Note that the printed string doesn't need to be the final concatenated string. It only needs to represent an unordered multiset of letters.

Examples

　　input

12

　　output

abababab

　　input

3

　　output

codeforces

Note

For the multiset {'a', 'b', 'a', 'b', 'a', 'b', 'a', 'b'}, one of the ways to complete the process is as follows:

• {"ab", "a", "b", "a", "b", "a", "b"}, with a cost of 0;
• {"aba", "b", "a", "b", "a", "b"}, with a cost of 1;
• {"abab", "a", "b", "a", "b"}, with a cost of 1;
• {"abab", "ab", "a", "b"}, with a cost of 0;
• {"abab", "aba", "b"}, with a cost of 1;
• {"abab", "abab"}, with a cost of 1;
• {"abababab"}, with a cost of 8.

The total cost is 12, and it can be proved to be the minimum cost of the process.

题目大意：要构造一个字符串(小写字母)，一开始字符串中的每个字符一行，要合并这些字符，使得完全合并后的价值为N。

试题分析：其实想想还是挺简单的，发现无论什么顺序最后每个字符出现次数相同的字符串都会的出来一样的结果。

　　　　　有了这个结论就很好做了，可以发现连续k个对于答案的贡献是k*(k-1)/2 ( (1+(k-1))*(k-1)/2 )

　　　　　预处理一下sum(1..i)，然后由剩下N的值二分一下，不必担心超过26个字符

代码：

#include<iostream>
#include<cstring>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;

#define LL long long

inline int read(){
	int x=0,f=1;char c=getchar();
	for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
	for(;isdigit(c);c=getchar()) x=x*10+c-'0';
	return x*f;
}
const int INF=9999999;
const int MAXN=100000;

int N;
int a[MAXN+1];
int tmp; int num[MAXN+1];

int main(){
	N=read();
	if(!N){
		puts("ab");
		return 0;
	}
	for(int i=1;i<=10000;i++) a[i]=a[i-1]+i;
	while(N){
		int k=lower_bound(a+1,a+10001,N)-a;
		if(a[k]!=N) k--;
		N-=a[k];
		num[tmp]=k+1;
		++tmp;
	}
	for(int i=0;i<tmp;i++) {
		for(int j=1;j<=num[i];j++)
		    printf("%c",'a'+i);
	}
	return 0;
}