FM算法(一)：算法理论

主要内容：

动机
FM算法模型
FM算法VS 其他算法

一、动机

在传统的线性模型如LR中，每个特征都是独立的，如果需要考虑特征与特征直接的交互作用，可能需要人工对特征进行交叉组合；非线性SVM可以对特征进行kernel映射，但是在特征高度稀疏的情况下，并不能很好地进行学习；现在也有很多分解模型Factorization model如矩阵分解MF、SVD++等，这些模型可以学习到特征之间的交互隐藏关系，但基本上每个模型都只适用于特定的输入和场景。为此，在高度稀疏的数据场景下如推荐系统，FM（Factorization Machine）出现了。

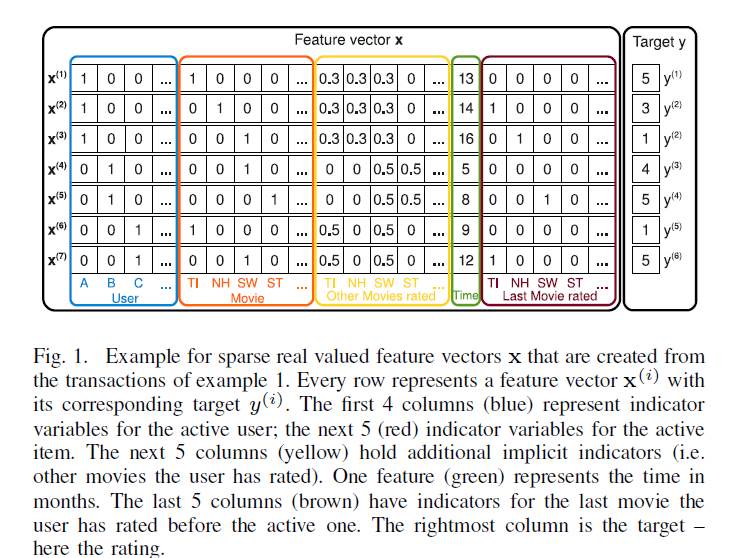
下面所有的假设都是建立在稀疏数据的基础上，举个例子，根据用户的评分历史预测用户对某部电影的打分，这里的每一行对应一个样本，Feature vector x表示特征，Targer y表示预测结果。从下图可以看出，这是一个稀疏特征的例子，后面的相关内容会以此为例子进行说明。

特征中的前四列表示用户u（one-hot编码，稀疏），接着五列表示电影i（ont-hot编码，稀疏），再接下去五列表示用户u对电影i的打分（归一化特征），紧接着一列表示时间（连续特征），最后五列表示用户u对电影i打分前评价过的最近一部电影（one-hot编码，稀疏）

二、FM算法模型

1、模型目标函数

二元交叉的FM（2-way FM）目标函数如下：

其中，w是输入特征的参数，<vi,vj>是输入特征i,j间的交叉参数，v是k维向量。

前面两个就是我们熟知的线性模型，后面一个就是我们需要学习的交叉组合特征，正是FM区别与线性模型的地方。

为什么要通过向量v的学习方式而不是简单的wij参数呢？

这是因为在稀疏条件下，这样的表示方法打破了特征的独立性，能够更好地挖掘特征之间的相关性。以上述电影为例，我们要估计用户A和电影ST的关系w(A&ST)以更好地预测y，如果是简单地考虑特征之间的共现情况来估计w(A&ST)，从已有的训练样本来看，这两者并没有共现，因此学习出来的w(A&ST)=0。而实际上，A和ST应该是存在某种联系的，从用户角度来看，A和B都看过SW，而B还看过ST，说明A也可能喜欢ST，说明A很有可能也喜欢ST。而通过向量v来表示用户和电影，任意两两之间的交互都会影响v的更新，从前面举的例子就可以看过，A和B看过SW，这样的交互关系就会导致v(ST)的学习更新，因此通过向量v的学习方式能够更好的挖掘特征间的相互关系，尤其在稀疏条件下。

2、模型的计算复杂度

可能有人会问，这样两两交叉的复杂度应该O(k*n^2)吧，其实，通过数学公式的巧妙转化一下，就可以变成O(kn)了。转化公式如下所示，其实就是利用了2xy = (x+y)^2 – x^2 – y^2的思路。

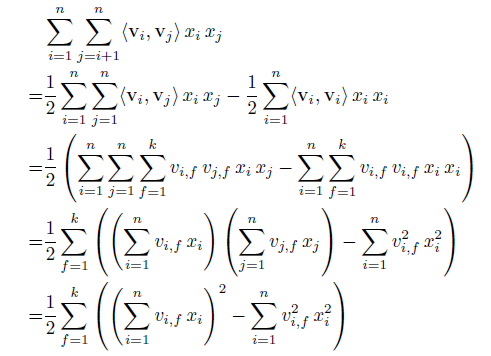
3、模型的应用

FM可以应用于很多预测任务，比如回归、分类、排序等等。

1.回归Regression：y^(x)直接作为预测值，损失函数可以采用least square error；

2.二值分类Binary Classification：y^(x)需转化为二值标签，如0,1。损失函数可以采用hinge loss或logit loss；

3.排序Rank：x可能需要转化为pair-wise的形式如(X^a,X^b)，损失函数可以采用pairwise loss

4、模型的学习方法

前面提到FM目标函数可以在线性时间内完成，那么对于大多数的损失函数而言，FM里面的参数w和v更新通过随机梯度下降SGD的方法同样可以在线性时间内完成，比如logit loss，hinge loss，square loss，模型参数的梯度计算如下：

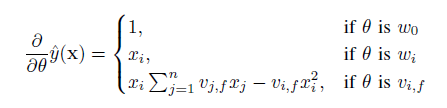
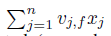这部分求和跟样本i是独立的，因此可以预先计算好。

5、模型延伸：多元交叉

前面提到到都是二元交叉，其实可以延伸到多元交叉，目标函数如下：（看起来复杂度好像很高，其实也是可以在线性时间内完成的）

6、总结

前面简单地介绍了FM模型，总的来说，FM通过向量交叉学习的方式来挖掘特征之间的相关性，有以下两点好处：

1.在高度稀疏的条件下能够更好地挖掘数据特征间的相关性，尤其是对于在训练样本中没出现的交叉数据；

2.FM在计算目标函数和在随机梯度下降做优化学习时都可以在线性时间内完成。

三、FM算法 VS 其他算法

1、FM 对比 SVM

1）SVM

SVM是大家熟知的支持向量机模型，其模型原理在这里就不详述了。

SVM的线性模型函数表示为：

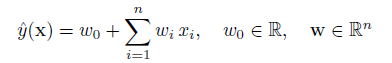
其非线性形式可以通过核映射kernel mapping的方式得到，如下所示：

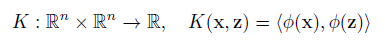
其中多项式核表示为：

当d=2时为二次多项式，表示为：

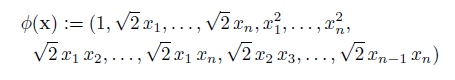
多项式核映射后的模型函数表示为：

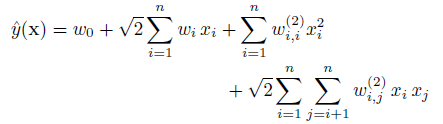
2）FM 对比 SVM

看到上面的式子，是不是觉得跟FM特别像？SVM和FM的主要区别在于，SVM的二元特征交叉参数是独立的，如wij，而FM的二元特征交叉参数是两个k维的向量vi、vj，这样子的话，<vi,vj>和<vi,vk>就不是独立的，而是相互影响的。

为什么线性SVM在和多项式SVM在稀疏条件下效果会比较差呢？线性svm只有一维特征，不能挖掘深层次的组合特征在实际预测中并没有很好的表现；而多项式svn正如前面提到的，交叉的多个特征需要在训练集上共现才能被学习到，否则该对应的参数就为0，这样对于测试集上的case而言这样的特征就失去了意义，因此在稀疏条件下，SVM表现并不能让人满意。而FM不一样，通过向量化的交叉，可以学习到不同特征之间的交互，进行提取到更深层次的抽象意义。

此外，FM和SVM的区别还体现在：1）FM可以在原始形式下进行优化学习，而基于kernel的非线性SVM通常需要在对偶形式下进行；2）FM的模型预测是与训练样本独立，而SVM则与部分训练样本有关，即支持向量。

2、FM 对比其他分解模型Fac torization Model

这部分不详述，其他分解模型包括Matrix factorization (MF)、SVD++、PITF for Tag Recommendation、Factorized Personalized Markov Chains (FPMC)，这些模型都只在特定场景下使用，输入形式也比较单一（比如MF只适用于categorical variables），而FM通过对输入特征进行转换，同样可可以实现以上模型的功能，而且FM的输入可以是任意实数域的数据，因此FM是一个更为泛化和通用的模型。详细内容参考：https://www.csie.ntu.edu.tw/~b97053/paper/Rendle2010FM.pdf

四、参考文献

1、《Factorization Machines》