【Notes_8】现代图形学入门——几何(基本表示方法、曲线与曲面)

几何

几何表示

隐式表示

不给出点的坐标，给数学表达式

优点 可以很容易找到点与几何之间的关系

缺点 找某特定的点很难

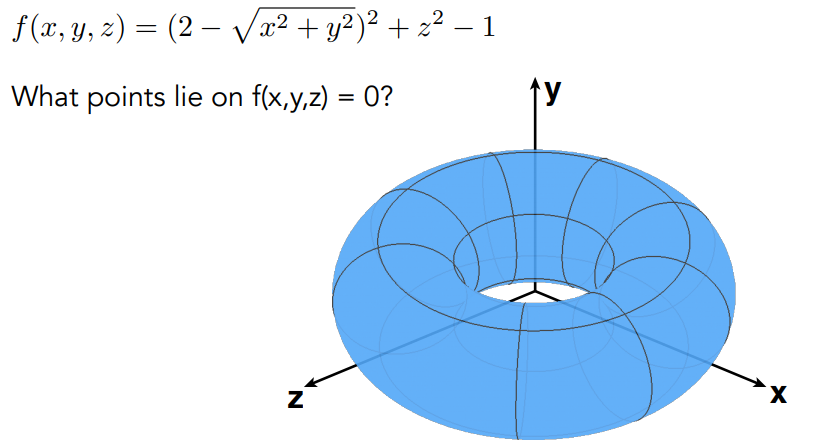
更多的隐式表示方法

Constructive Solid Geometry 、Distance Functions 、Level Set Methods 、Fractals

显示表示

直接给出点或者参数映射

优点 找某一点很容易

缺点 判断点与几何之间的关系很困难

更多的显式表示方法

Triangle meshes 、Bezier surfaces 、Subdivision surfaces 、NURBS 、Point clouds。

其中需要强调的一点在图形学中，显示存储在文件的格式是wavefront object file。

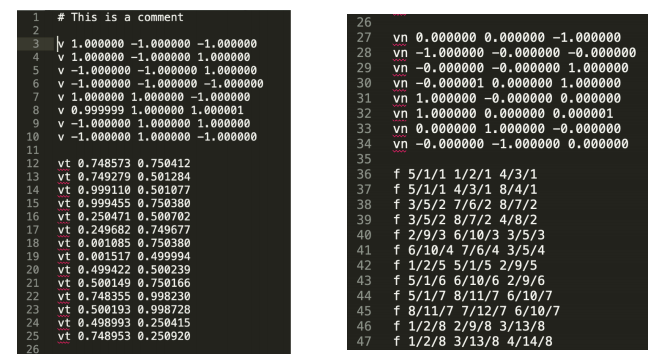
其中，\(v：\)顶点、\(v_n：\)法线、\(v_t：\)纹理坐标、\(f\)参数详解：(顶点坐标 纹理坐标 法线坐标)

曲线与曲面

贝塞尔曲线(Bézier Curves)

贝塞尔曲线是计算机图形图像造型的基本工具，是图形造型运用得最多的基本线条之一，是依据四个位置任意的点坐标绘制出的一条光滑曲线。

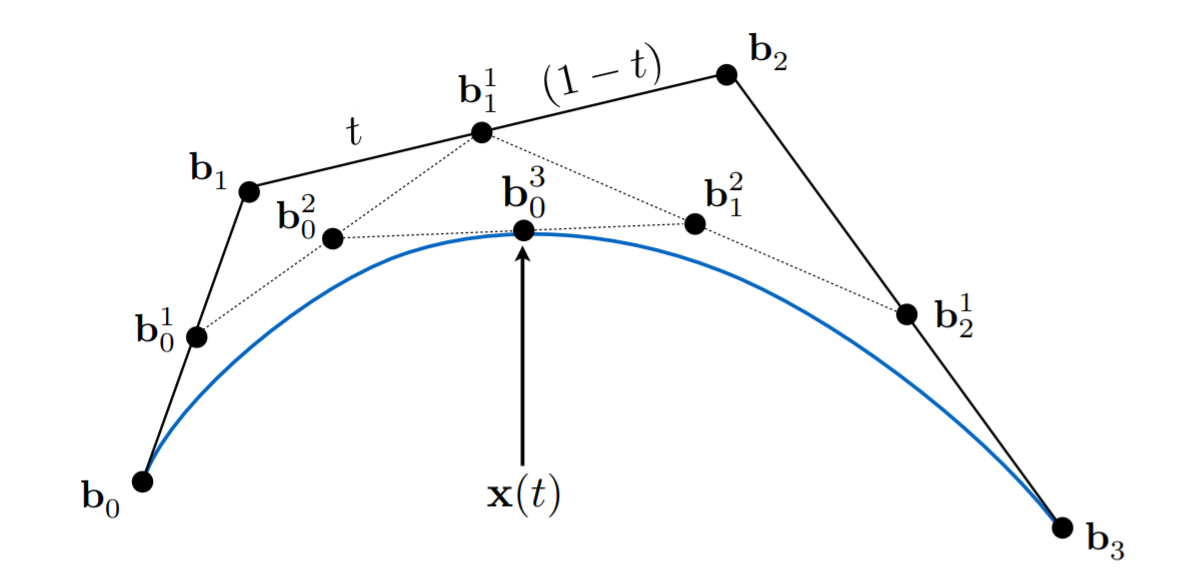
代数表示

主要是通过反复迭代实现，循环体是每两个点之间的通过特定的比例 \(t\) ，得到一个新的点；终止条件是最后只有一个点。

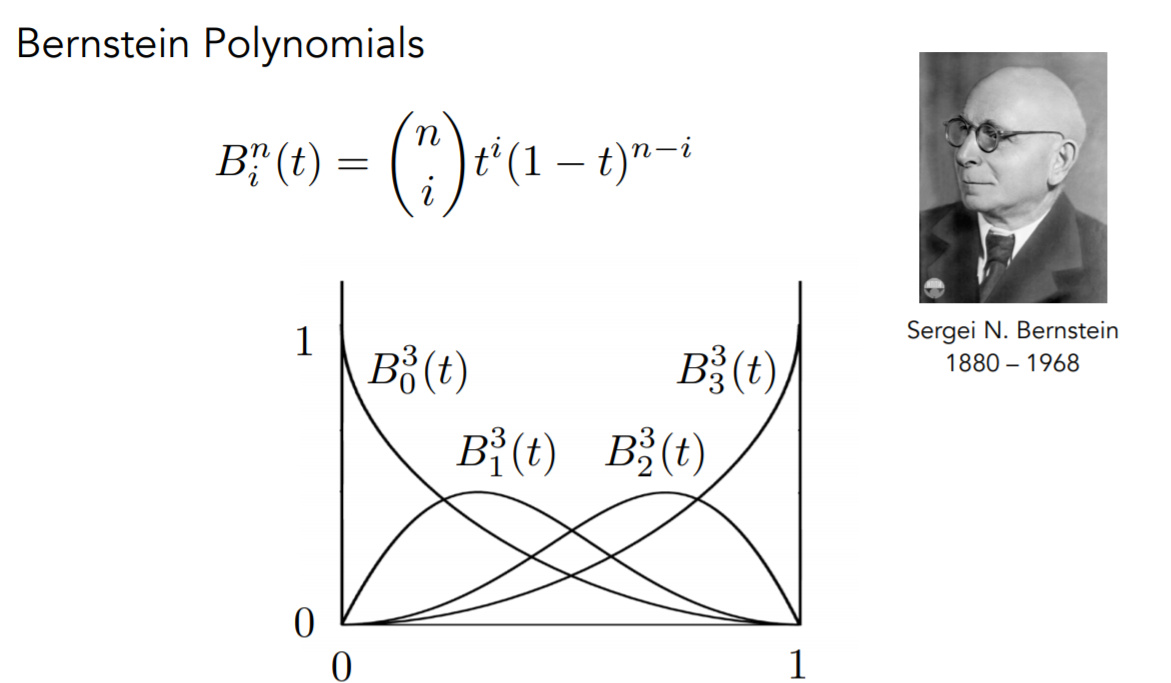
贝塞尔曲线性质

1. 端点性质

顶点P0和Pn分别位于曲线段的起点和终点上，曲线不通过其他控制点，即“逼近”而非“插值”。

2. 一阶导数

• Bernstein基函数的一阶导数为

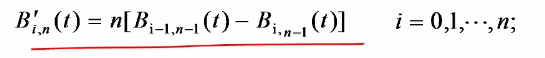
• Bezier曲线的一阶导数为

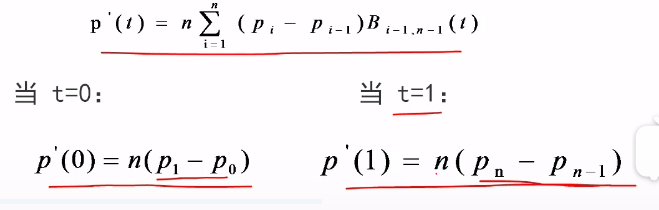
Bezier曲线的起点和终点处的切线方向和特征多边形的第一条边及最后一条线的走向一致。

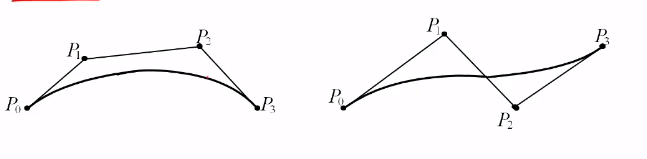
3. 几何不变性

指某些几何特性不随坐标变换而变化的特性。Bezier曲线的形状仅与控制多边形各顶点的相对位置有关，而与坐标系的选择无关。

4. 凸包性

Bezier曲线落在控制点Pi构成的凸包内

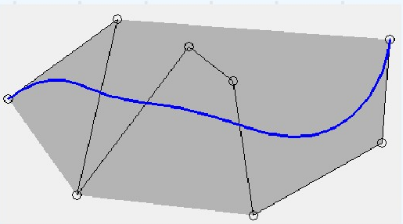
分段贝塞尔曲线

当控制贝塞尔曲线的控制点多的时候，可以通过分段生成贝塞尔曲线来实现。

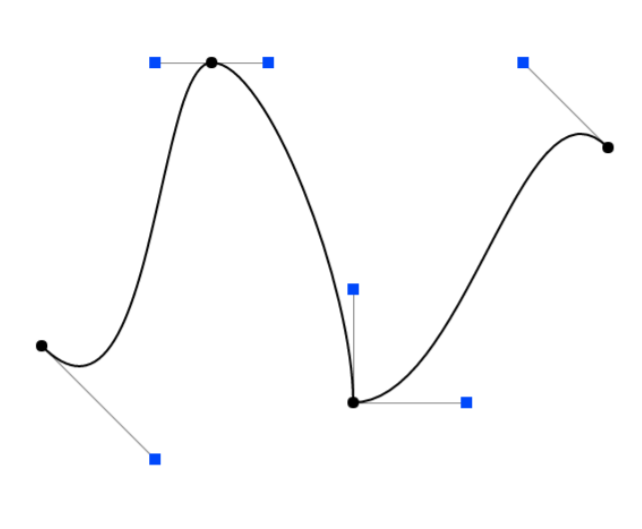
贝塞尔曲线拼接

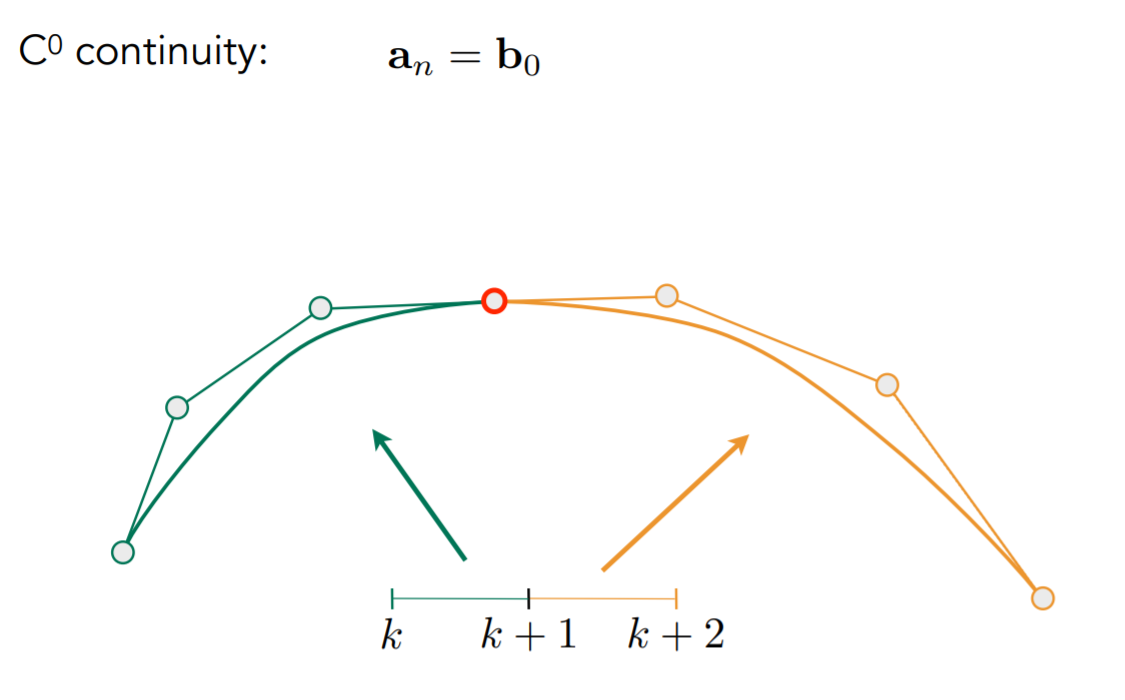
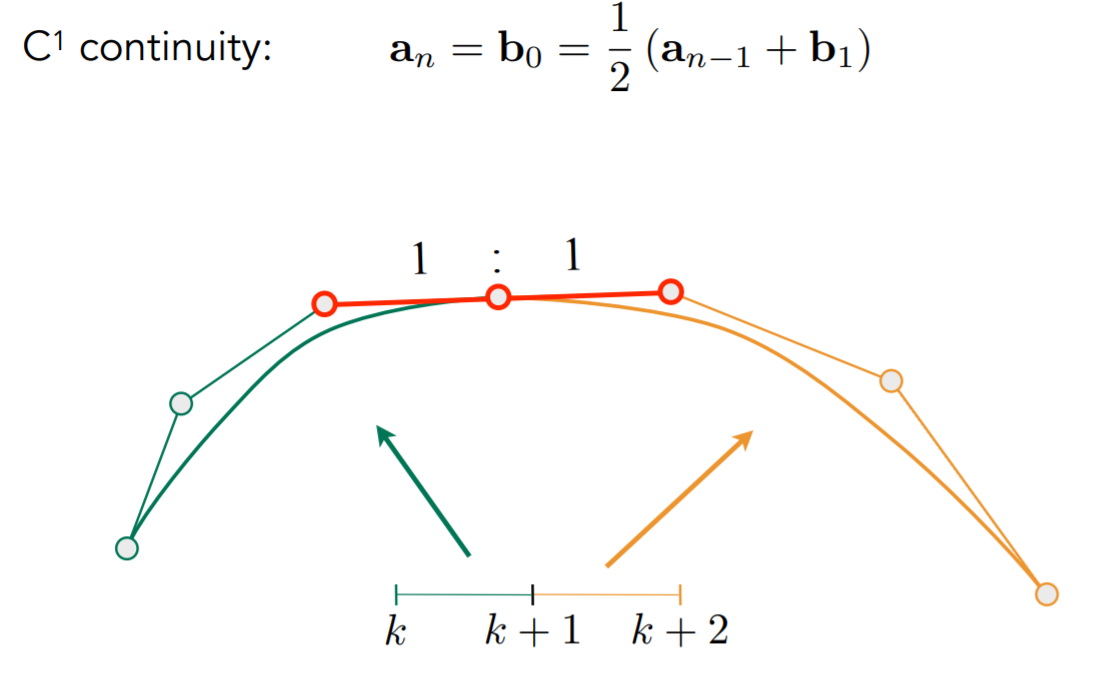
贝塞尔曲面

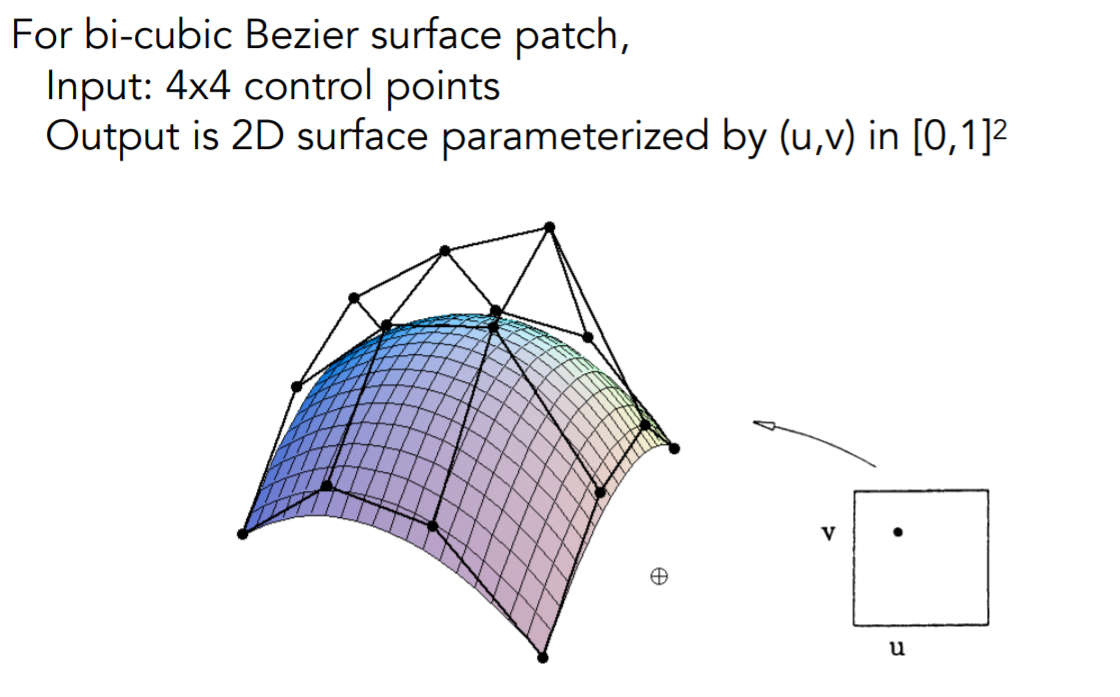
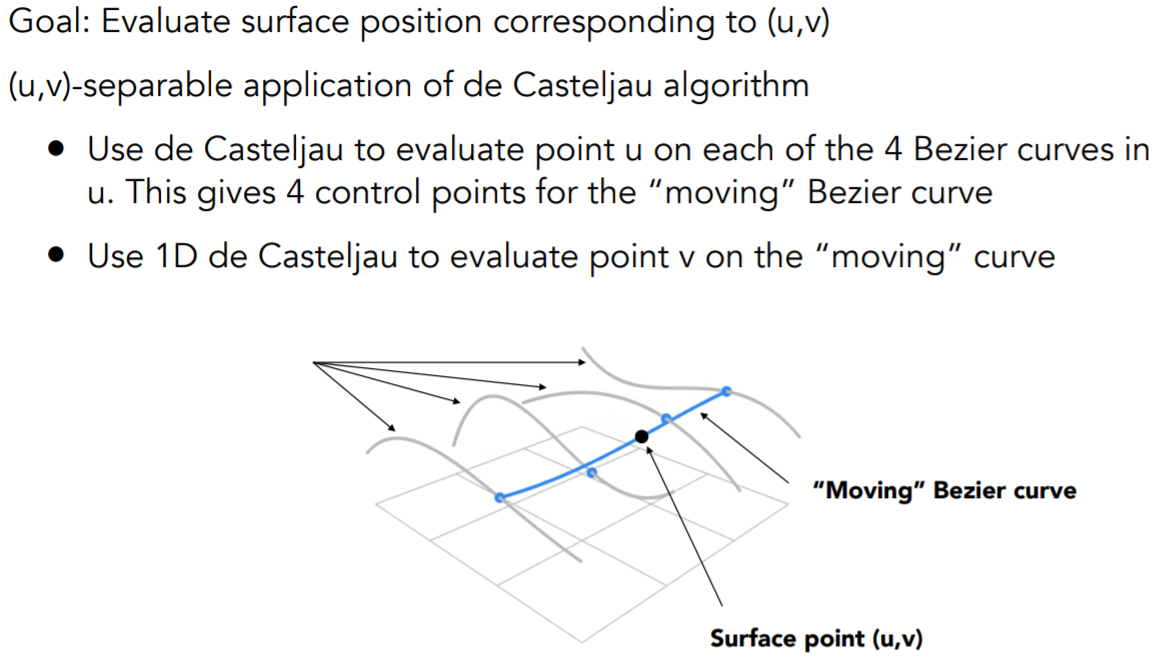
几何操作

曲面的几何操作主要有：曲面细分、曲面简化、曲面正则化。

曲面细分

曲面细分主要有以下两个主要的步骤：1.创建更多的面(顶点) 2.移动面(顶点)的位置

Loop Subdivision

Loop Subdivision主要是针对三角形曲面的细分

1. 创建更多的面(顶点)

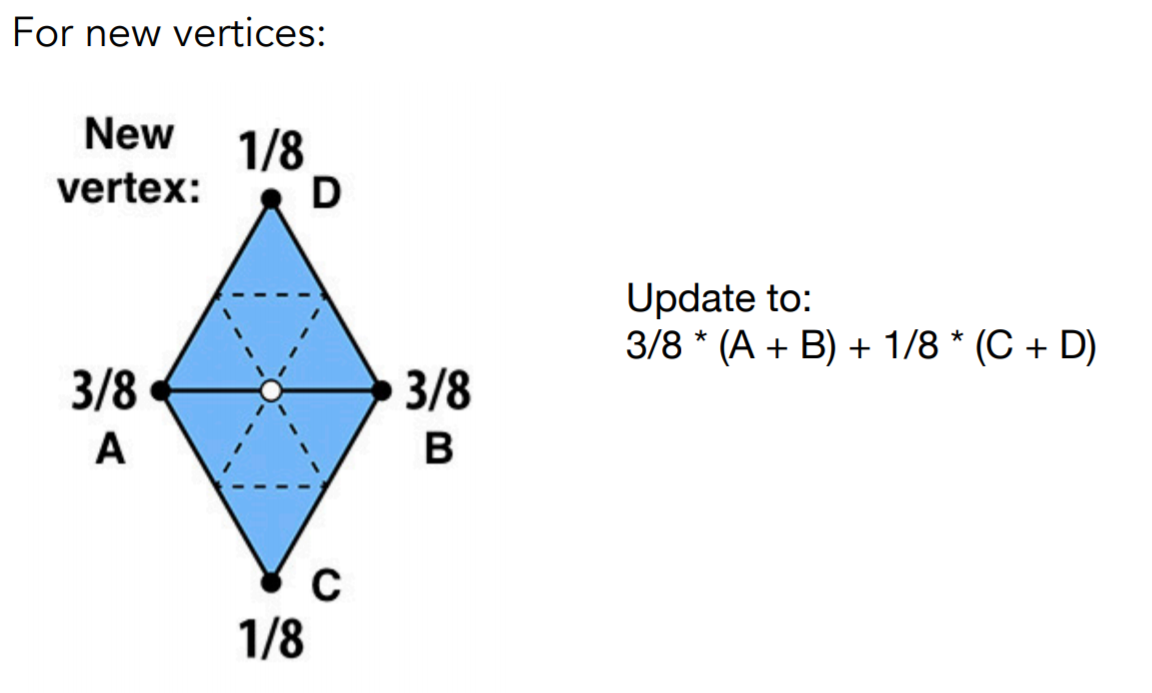
2. 移动顶点的位置

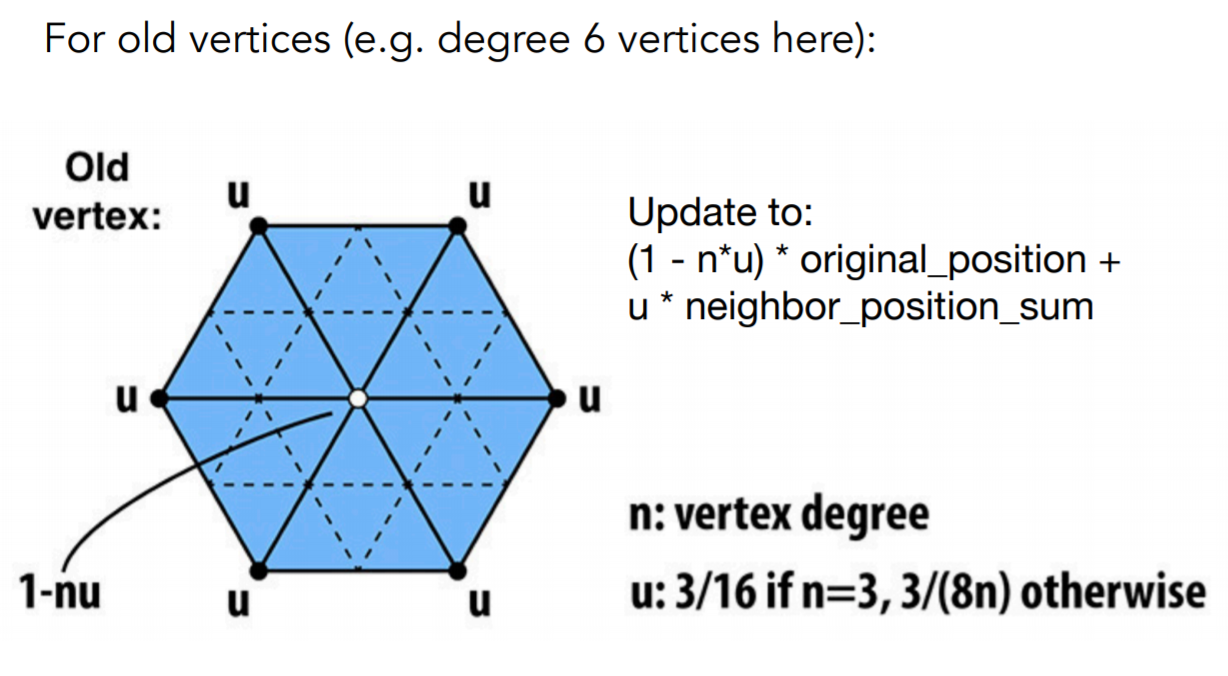
Catmull

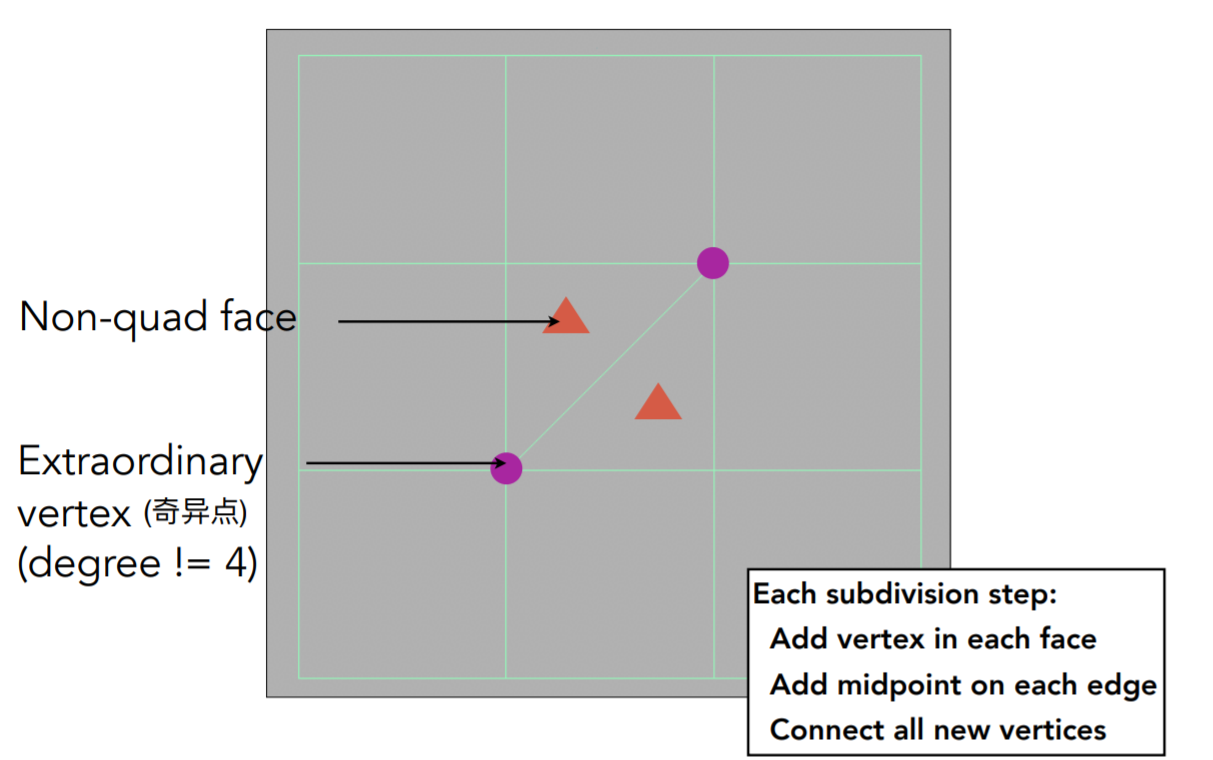
奇异点：与点相连接的边不为4的点

face point：每个面中的点，用周围点的平均值代表

曲面简化