死磕HashMap

前言

HashMap是Java中最常用的集合类框架，也是Java语言中非常典型的数据结构，同时也是我们需要掌握的数据结构，更重要的是进大厂面试必问之一。

数组特点

存储区间是连续，且占用内存严重，空间复杂也很大，时间复杂为O（1）。

优点：是随机读取效率很高，原因数组是连续（随机访问性强，查找速度快）。

缺点：插入和删除数据效率低，因插入数据，这个位置后面的数据在内存中要往后移的，且大小固定不易动态扩展。

链表特点

区间离散，占用内存宽松，空间复杂度小，时间复杂度O(N)。

优点：插入删除速度快，内存利用率高，没有大小固定，扩展灵活。

缺点：不能随机查找，每次都是从第一个开始遍历（查询效率低）。

哈希表特点

以上数组和链表，大家都知道各自优缺点。那么我们能不能把以上两种结合一起使用，从而实现查询效率高和插入删除效率也高的数据结构呢？答案是可以滴，那就是哈希表可以满足，接下来我们一起复习HashMap中的put()和get()方法实现原理。

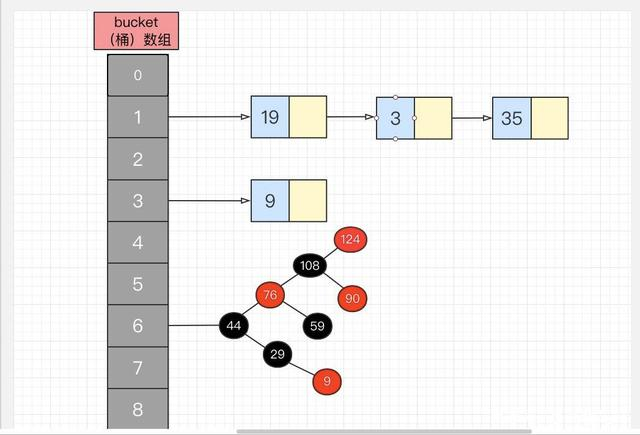
JDK1.8中堆HashMap做了一下改动：

1）默认初始化容量=0

2）引入红黑树，优化数据结构

3) 将链表头插法改为尾插法，解决1.7中多线程循环链表的bug

4）优化hash算法

5）resize计算索引位置的算法改进

6）先插入后扩容

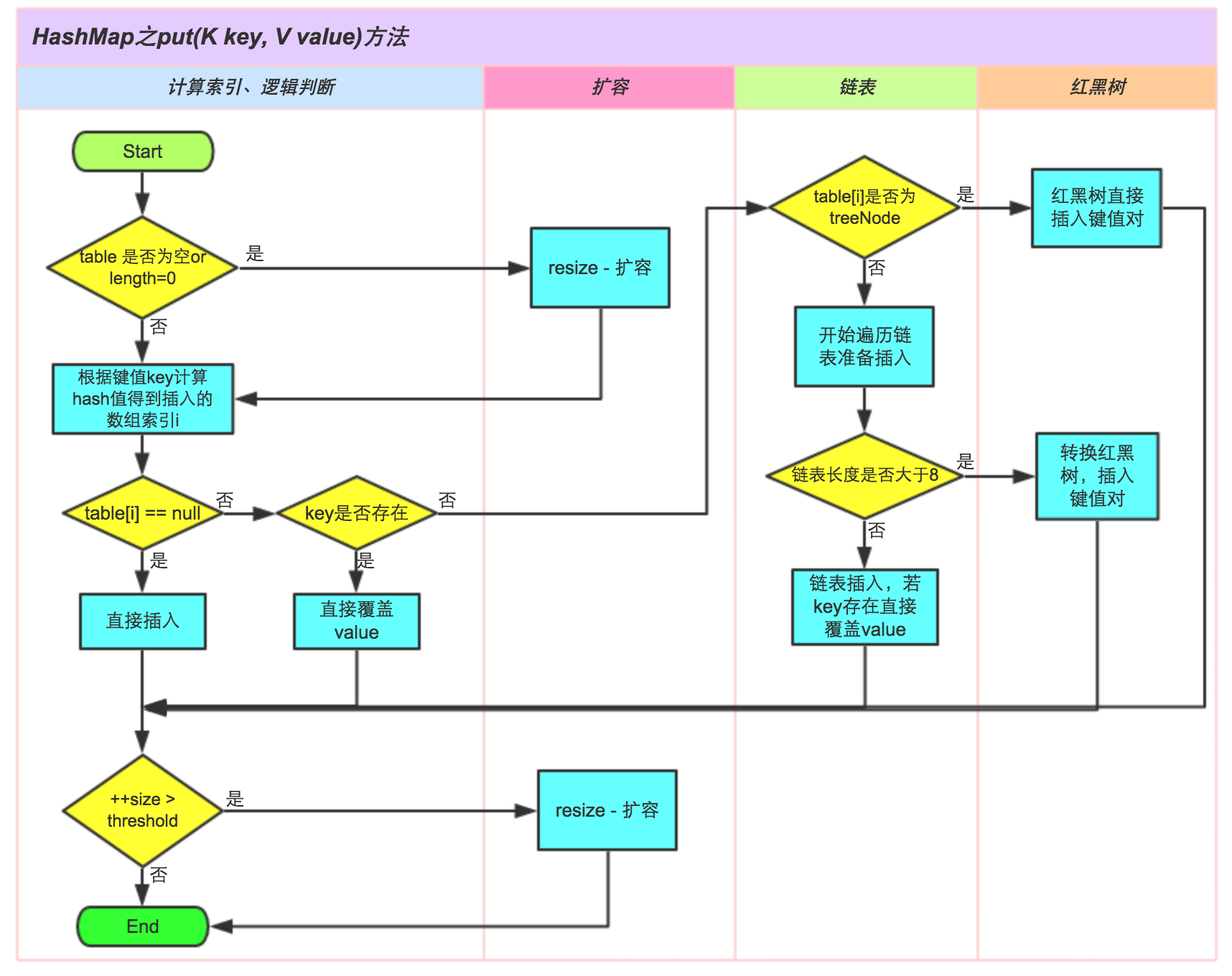
Hashmap 中put()过程

 public V put(K key, V value) {
        return putVal(hash(key), key, value, false, true);
    }
    final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
                   boolean evict) {
        Node<K,V>[] tab; Node<K,V> p; int n, i;
        // 判断数组是否为空，长度是否为0，是则进行扩容数组初始化
        if ((tab = table) == null || (n = tab.length) == 0)
            n = (tab = resize()).length;
        // 通过hash算法找到数组下标得到数组元素，为空则新建
        if ((p = tab[i = (n - 1) & hash]) == null)
            tab[i] = newNode(hash, key, value, null);
        else {
            Node<K,V> e; K k;
            // 找到数组元素，hash相等同时key相等，则直接覆盖
            if (p.hash == hash &&
                ((k = p.key) == key || (key != null && key.equals(k))))
                e = p;
            // 该数组元素在链表长度>8后形成红黑树结构的对象,p为树结构已存在的对象
            else if (p instanceof TreeNode)
                e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
            else {
                // 该数组元素hash相等，key不等，同时链表长度<8.进行遍历寻找元素，有就覆盖无则新建
                for (int binCount = 0; ; ++binCount) {
                    if ((e = p.next) == null) {
                        // 新建链表中数据元素，尾插法
                        p.next = newNode(hash, key, value, null);
                        if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                            // 链表长度>=8 结构转为 红黑树
                            treeifyBin(tab, hash);
                        break;
                    }
                    if (e.hash == hash &&
                        ((k = e.key) == key || (key != null && key.equals(k))))
                        break;
                    p = e;
                }
            }
            // 新值覆盖旧值
            if (e != null) { // existing mapping for key
                V oldValue = e.value;
                // onlyIfAbsent默认false
                if (!onlyIfAbsent || oldValue == null)
                    e.value = value;
                afterNodeAccess(e);
                return oldValue;
            }
        }
        ++modCount;
        // 判断是否需要扩容
        if (++size > threshold)
            resize();
        afterNodeInsertion(evict);
        return null;
    }

基本过程如下：

1）检查数据是否，执行resize()扩容，在实例化HashMap时，并不会进行初始化数组

2）通过hash值计算数组索引，获取该索引位的首节点

3）如果首节点为null，则创建新的数组元素，直接添加节点到该索引位（bucket）

4）如果首节点不为null，那么还有三种情况

1）key和首节点的key相同，覆盖old value(保证key的唯一性),否则执行2或者3

2) 如果首节点是红黑树(TreeNode),将键值对添加到红黑树

3）如果首节点是链表，进行遍历寻找元素，有就覆盖无则新建，将键值对添加到链表，添加后会判断链表长度是否达到TREEIFY_THRESHOLD-1                           的 阈值，尝试将链表转换成红黑树。

5) 判断当前元素个数是否大于threshold，扩充数组

Hashmap 中get()过程

 

public V get(Object key) {
        Node<K,V> e;
        return (e = getNode(hash(key), key)) == null ? null : e.value;
    }

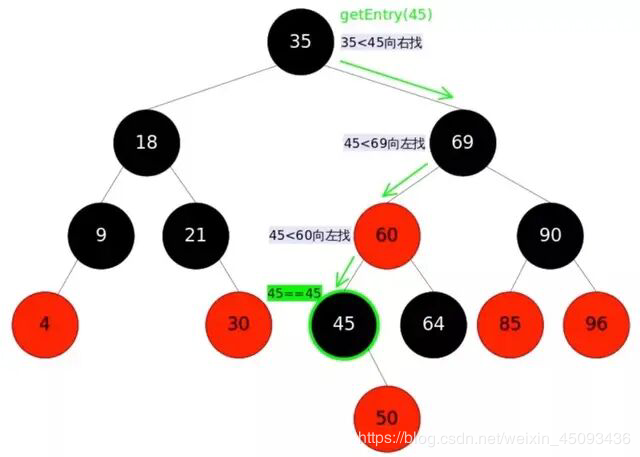
    final Node<K,V> getNode(int hash, Object key) {
        Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
        if ((tab = table) != null && (n = tab.length) > 0 &&
            (first = tab[(n - 1) & hash]) != null) {
            // 永远检查第一个node
            if (first.hash == hash && // always check first node
                ((k = first.key) == key || (key != null && key.equals(k))))
                return first;
            if ((e = first.next) != null) {
                if (first instanceof TreeNode)  // 树查找
                    return ((TreeNode<K,V>)first).getTreeNode(hash, key);
                do {
                    if (e.hash == hash &&   // 遍历链表
                        ((k = e.key) == key || (key != null && key.equals(k))))
                        return e;
                } while ((e = e.next) != null);
            }
        }
        return null;
    }

1.8以后，无论是存元素还是取元素，都是优先判断bucket上第一个元素是否匹配，而在1.7中则是直接遍历查找

基本过程：

1）根据key计算hash

2）检查数组是否为空，为空则返回null，

3）根据hash计算bucket位置，如果bucket第一个元素是目标元素，则直接返回，否则执行4

4）如果bucket上元素大于1 并且是树结构，则执行树查找，否则执行5

5) 如果是链表结构，则遍历寻找目标

Hashmap 中resize()过程

 

 final Node<K,V>[] resize() {
        Node<K,V>[] oldTab = table;
        int oldCap = (oldTab == null) ? 0 : oldTab.length;
        int oldThr = threshold;
        int newCap, newThr = 0;
        if (oldCap > 0) {
            // 如果已达到最大容量不在扩容
            if (oldCap >= MAXIMUM_CAPACITY) {
                threshold = Integer.MAX_VALUE;
                return oldTab;
            }
            // 通过位运算扩容到原来的两倍
            else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
                     oldCap >= DEFAULT_INITIAL_CAPACITY)
                newThr = oldThr << 1; // double threshold
        }
        else if (oldThr > 0) // initial capacity was placed in threshold
            newCap = oldThr;
        else {               // zero initial threshold signifies using defaults
            newCap = DEFAULT_INITIAL_CAPACITY;
            newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
        }
        if (newThr == 0) {
            float ft = (float)newCap * loadFactor;
            newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
                      (int)ft : Integer.MAX_VALUE);
        }
        // 新的扩容临界值
        threshold = newThr;
        @SuppressWarnings({"rawtypes","unchecked"})
            Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
        table = newTab;
        if (oldTab != null) {
            for (int j = 0; j < oldCap; ++j) {
                Node<K,V> e;
                if ((e = oldTab[j]) != null) {
                    oldTab[j] = null;
                    // 如果该位置元素没有next节点，将该元素放入新数组
                    if (e.next == null)
                        newTab[e.hash & (newCap - 1)] = e;
                    else if (e instanceof TreeNode)
                        // 树节点
                        ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
                    else { // preserve order
                        // 链表节点。

                        // lo串的新索引位置与原先相同
                        Node<K,V> loHead = null, loTail = null;
                        // hi串的新索引位置为[原先位置j+oldCap]
                        Node<K,V> hiHead = null, hiTail = null;
                        Node<K,V> next;
                        do {
                            next = e.next;
                            // 原索引，oldCap是2的n次方，二进制表示只有一个1，其余是0
                            if ((e.hash & oldCap) == 0) {
                                if (loTail == null)
                                    loHead = e;
                                else
                                    // 尾插法
                                    loTail.next = e;
                                loTail = e;
                            }
                            // 原索引+oldCap
                            else {
                                if (hiTail == null)
                                    hiHead = e;
                                else
                                    hiTail.next = e;
                                hiTail = e;
                            }
                        } while ((e = next) != null);
                        // 根据hash判断该bucket上的整个链表的index还是旧数组的index，还是index+oldCap
                        if (loTail != null) {
                            loTail.next = null;
                            newTab[j] = loHead;
                        }
                        if (hiTail != null) {
                            hiTail.next = null;
                            newTab[j + oldCap] = hiHead;
                        }
                    }
                }
            }
        }
        return newTab;
    }

1.8版本中扩容相对复杂，在1.7版本中，重新根据hash计算索引位置即可，而在1.8版本中分为2中情况

     链转树，树转表

           当 元素长度大于64同时hash冲突大于8，则会把链表转成红黑树，

          当红黑树元素数少于6，则会转成链表

     个人理解是，当元素个数小于6之后，链表的遍历速度是优于红黑树的，大于8之后，红黑树遍历速度是高于链表的速度， 

     当然了，据说是数据科学家根据概率做出的经验值，同时避免数据结构频繁的转换引起的性能开销

为什么要引入红黑树？

在jdk1.8引入了红黑树的设计，当冲突的链表长度超过8个时，链表结构就会转为红黑树结构，这样做的好处是避免在极端条件的情况下冲突链表过长而导致查询效率非常慢。

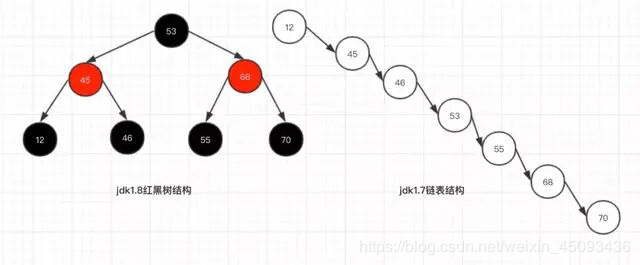
红黑树查询：其访问性能近似于折半查找，时间复杂度O(logn)

链表查询：这种情况下，需要遍历全部元素才行，时间复杂度O(n)

红黑树的简单概念

红黑树是一种近似平衡的二叉查找树，其主要的有点就是平衡，即左右子树高度几乎一致，以此来防止树退化为链表，通过这种方式来保障查找的时间复杂度为log(n）

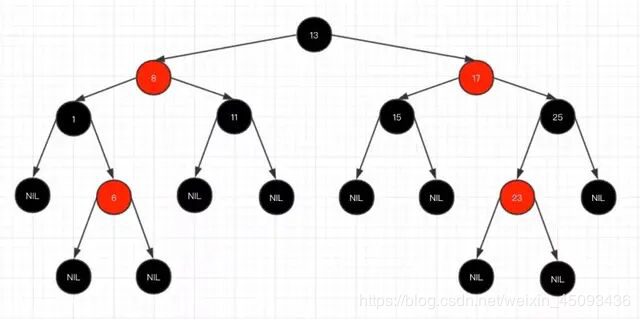
　　　　树的基本特征：

1）每个节点要么是黑色，要么是红色的，但根节点必须是黑色的

2）每个红色节点的两个子节点必须是黑色的

3）红色节点不能连续（即红色节点的孩子和父亲都不能是红色的）

4）从任意节点到其子树中每个叶子节点的路径都包含相同数量的黑色节点

5）所有的叶子节点都是黑色的

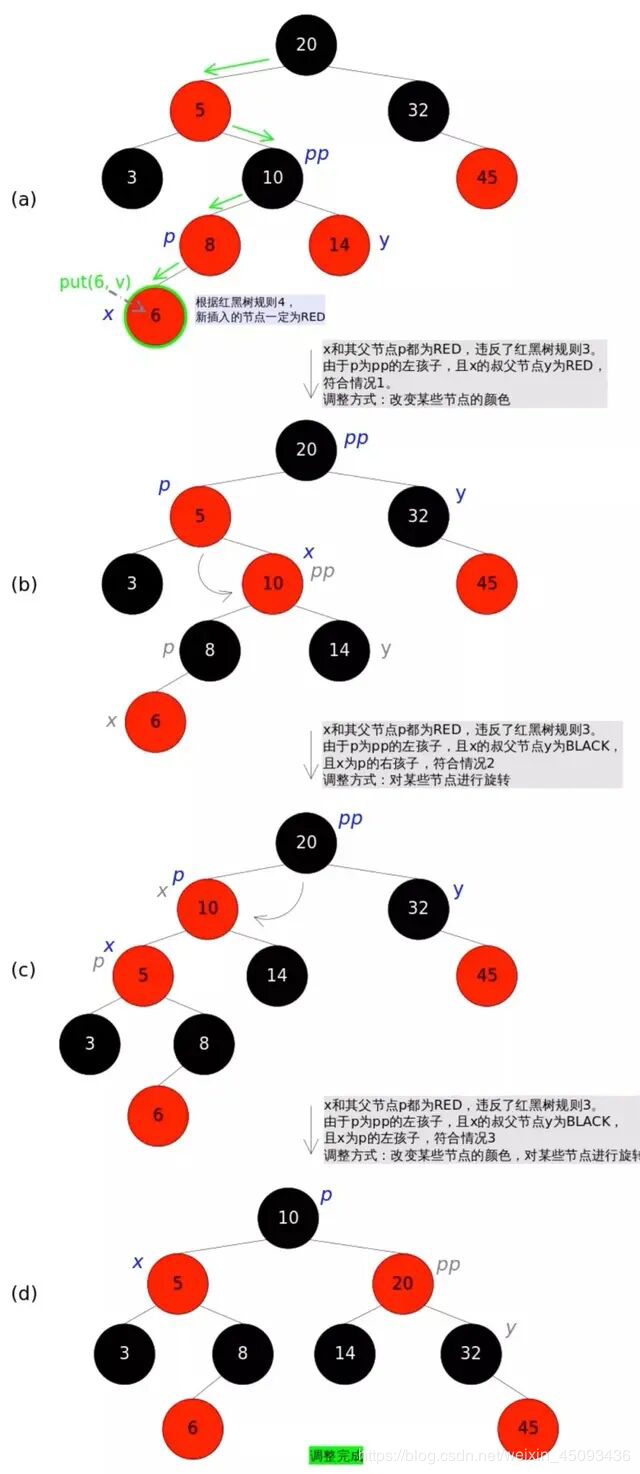
6）新加入的红黑树的节点为红色节点

在树的结构发生改变时，往往会破坏条件3,4，需要通过调整使得查找树重新满足红黑树的条件

红黑树的调整方式

调整可以分为两类：

一类是颜色调整，即改变某个节点的颜色，这种比较简单，直接将节点颜色进行转换即可；

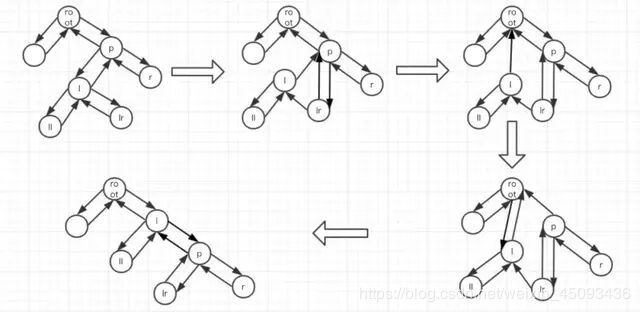
另一类是结构调整，改变检索树的结构关系。结构调整主要包含两个基本操作：左旋(Rotate Left),右旋(Rotate Right)。

1.左旋
                        左旋的过程是将p的右子树绕p逆时针旋转，使得p的右子树成为p的父亲，同时修改相关节点的引用，使得左子树的深度加1，右子树的深度减1，通过这种做法来调整树的稳定性。过程如下：

static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {         //指向父节点的指针         TreeNode<K,V> parent;
        //指向左孩子的指针 TreeNode<K,V> left;
        //指向右孩子的指针 TreeNode<K,V> right;
        //前驱指针，跟next属性相反的指向 TreeNode<K,V> prev;
        //是否为红色节点 boolean red;
        ...... }
//左旋方法如下
static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,
                                              TreeNode<K,V> p) {
            TreeNode<K,V> r, pp, rl;//p表示要调整的节点，r表示右节点，pp表示p的parent节点，rl表示p的右孩子的左孩子节点
            //r判断，如果r为空则旋转没有意义
            if (p != null && (r = p.right) != null) {
                //设置rl的父亲为p
                if ((rl = p.right = r.left) != null)
                    rl.parent = p;
                //判断p的父亲，为空，为根节点，根节点的话就设置为黑色
                if ((pp = r.parent = p.parent) == null)
                    (root = r).red = false;
                //判断p节点是左儿子还是右儿子
                else if (pp.left == p)
                    pp.left = r;
                else
                    pp.right = r;
                r.left = p;
                p.parent = r;
            }
            return root;
        }

右旋

static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root,
                                               TreeNode<K,V> p) {
            TreeNode<K,V> l, pp, lr;//lr表示p的左孩子的右孩子
            //l判断，如果l为空则旋转没有意义
            if (p != null && (l = p.left) != null) {
                //设置lr的父亲为p
                if ((lr = p.left = l.right) != null)
                    lr.parent = p;
                //判断p的父亲，为空，为根节点。根节点的话就设置为黑色
                if ((pp = l.parent = p.parent) == null)
                    (root = l).red = false;
                //判断p节点是左儿子还是右儿子
                else if (pp.right == p)
                    pp.right = l;
                else
                    pp.left = l;
                l.right = p;
                p.parent = l;
            }
            return root;
        }

关于红黑树的结构的调整流程，基本都是先调整结构，然后调整颜色，知道最后满足红黑树的特性要求

为什么HashMap使用红黑树而不使用AVL树

在CurrentHashMap中是加锁了的，实际上是读写锁，如果写冲突就会等待，如果插入时间过长必然等待时间更长，而红黑树相对AVL树，他的插入更快。

红黑树和AVL树都是常用的平衡二叉搜索树，它们的查找，删除，，修改都是0（longN）

AVL和红黑树有几点比较和区别：

1）AVL树是更加严格的平衡，因此可以提供更快的查找速度，一般读取查找密集型任务，使用AVL树

2）红黑树更适合于插入修改密集型任务

3）通常，avl树的旋转比红黑树的旋转更加难以平衡和调试

结论：

1）AVL以及红黑树是高度平衡的树数据结构，他们非常相似，真正的区别在于在任何添加/删除操作时完成的旋转次数

2）两种实现都缩放为a O（lgN），其中N是叶子的数量，但实际上AVL树在查找密集型任务上更快，利用更好的平衡，树遍历平均更短，

另一方面，插入和删除方面，AVL树速度较慢，需要更高的旋转次数才能在修改时正确得重新平衡数据结构

3）在AVL树中，从根到任何叶子的最短路径和最长路径之间的差异最多为1，在红黑树中，差异可以是2倍

4）两个都给0 （logN） 查找，但是平衡AVL树可能需要0（logN）旋转，而红黑树将需要最多两次旋转使其达到平衡，旋转本身是O（1）操作，因为你只是移动指针

HashMap的长度为什么要是2的n次方

HashMap为了存取高效，要尽量减少碰撞，就是要尽量把数据分配平均，每个链表长度大致相同，这个实现就在把数据存在哪个链表中的算法

这个算法实际就是取模，hash%length，计算机中直接求余效率不如位移运算，源码中做了优化 hash&（length-1）

hash%length==hash&(length-1) 的前提是length是2的n次方

为什么这样能均匀分布减少碰撞呢？2的n次方实际就是1后面n个0,2的n次方-1，实际就是n个1；

例如长度为9时候，3&（9-1）=0 2&（9-1）=0 ，都在0上 ，碰撞了

例如长度为8时， 3&（8-1）=3   2&（8-1）=2  ，不同位置，不碰撞

HashMap的默认长度为什么要是16

如果桶初始化数组设置太大，就会浪费内存空间，16应该会死一个折中的大小，不会像1,2,3那样放几个元素就扩容，也不会像几千几万那样可以只会利用一点点空间从而造成大量的浪费。

HashMap为什么线程不安全

Java7在多线程操作HashMap时可能引起死循环，原因是扩容转移后前后链表顺序倒置，在转移过程中修改了原来链表中节点的引用关系。

Java8在同样的前提下并不会引起死循环，原因是扩容转移后前后链表顺序不变，保持之前节点的引用关系。

但是即使不会出现死循环，但是通过源码看到put/get方法都没有加同步锁，多线程情况最容易出现的就是：无法保证上一秒put的值，下一秒get的时候还是原值，所以线程安全还是无法保证。

HashMap会进行resize(扩容)操作，重新计算hash值，在resize操作的时候会造成线程不安全。下面将举两个可能出现线程不安全的地方。

1、put的时候导致的多线程数据不一致。
这个问题比较好想象，比如有两个线程A和B，首先A希望插入一个key-value对到HashMap中，首先计算记录所要落到的桶的索引坐标，然后获取到该桶里面的链表头结点，此时线程A的时间片用完了，而此时线程B被调度得以执行，和线程A一样执行，只不过线程B成功将记录插到了桶里面，假设线程A插入的记录计算出来的桶索引和线程B要插入的记录计算出来的桶索引是一样的，那么当线程B成功插入之后，线程A再次被调度运行时，它依然持有过期的链表头但是它对此一无所知，以至于它认为它应该这样做，如此一来就覆盖了线程B插入的记录，这样线程B插入的记录就凭空消失了，造成了数据不一致的行为。

2、另外一个比较明显的线程不安全的问题是HashMap的get操作可能因为resize而引起死循环（cpu100%），即产生链表循环引用的现象（jdk7）

HashMap 如何变成线程安全的

currentHashMap 以及 hashTable，Collections.synchronizeMap(),或者直接枷锁