化繁为简 经典的汉诺塔递归问题 in Java

---

问题描述

  在世界中心贝拿勒斯（在印度北部）的圣庙里，一块黄铜板上插着三根宝石针。印度教的主神梵天在创造世界的时候，在其中一根针上从下到上地穿好了由大到小的64片金片，这就是所谓的汉诺塔。不论白天黑夜，总有一个僧侣在按照下面的法则移动这些金片：一次只移动一片，不管在哪根针上，小片必须在大片上面。僧侣们预言，当所有的金片都从梵天穿好的那根针上移到另外一根针上时，世界就将在一声霹雳中消灭，而梵塔、庙宇和众生也都将同归于尽。

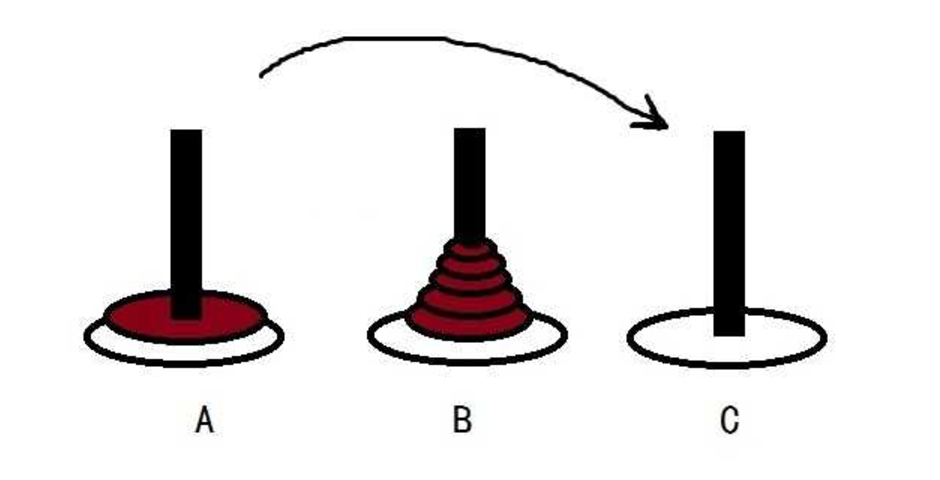
  扯远了，把这个问题简单描述下有A,B,C三根柱子，将A柱上N个从小到大叠放的盘子移动到C柱，一次只能移动一个，不重复移动，小盘子必须在大盘子上面。

   问一共需要移动多少次,步骤是什么?

解决思路

让我们从简单的情况下开始考虑

首先我说明几个数学符号，我自己瞎编的，为了方便表示问题，不用打那么多字

• A -> B 箭头意思代表是从 A柱 移动到 B柱 ,每次移动都是移动最上面的那一块

n = 1

• 只有一个盘子的时候，很简单，直接移就是了，用数学符号记录一下代表 A -> C

n = 2

• 如果有两个盘子,就分为三步
  
  1.先将最上面的盘子也就是(从下往上数)第2个盘子,先移动到B 记为 A -> B
  
  2.然后将第一个盘子移动移动到C , A -> C
  
  3.最后将 B柱子上的盘子 移动到 C柱 , B -> C

n = 3

• 如果有三个盘子,就分为7步,这里就不打字了，太累，用数学符号表示

1. A -> C
2. A -> B
3. C -> B
4. A -> C
5. B -> A
6. B -> C
7. A -> C

额，不要摆出一副黑人问号脸...，自己随便拿三个道具摆一摆就知道了

当你摆一摆的时候就知道，我知道了，一个盘子移动1次，二个盘子移动3次，三个盘子移动7次，四个盘子移动15次，N个盘子移动\(2^n - 1\)次!

恭喜你答对了！数学归纳法找规律不需多久就可以找到规律，但还有问题是究竟要怎么移呢?... 以及用程序怎么解决呢？

n = n....

抽象出这个问题

• 将问题抽象出来并且转化为数学模型或者公式，是解决现实生活中复杂问题的一个很好的解决办法，例如谷歌的翻译，大家都觉得很智能，自然语言的翻译从20世界60年代就开始研究了，具体细节这里不是重点，最后的解决思路是基于统计模型来解决的，也就是说，困扰了很多年的问题最后是抽象成一个概率论公式得以解决，事实上，众多复杂的问题最后进行抽象其实就是几个流程和公式而已，下面就以这个汉诺塔问题为例。

• 当有N个盘子的时候，似乎很难去想具体怎么实现，既然这么难想，就不用去想，首先这个问题，中有三个柱子，A,B,C，这里也太具体了，抽象一下，怎么抽象呢？假如这个问题只有2根柱子，你能完成吗？废话，肯定不行啊，我还需要一个柱子来辅助移动，所以这里的A,B,C三个柱子就抽象成，起始柱，中间柱，目标柱，这里用from,mid,to来表示

• ok，现在是盘子的数量抽象成了n，柱子也抽象成了,from,mid,to 三种柱子，下面对过程进行抽象，将n个盘子从 from 柱子 移动到 to 柱 ，其实总体来看是三步

1. 将n-1个盘子从 起始 柱 移动到 中间 柱
2. 将第n个盘子从 起始 柱 移动到 目标 柱
3. 将n-1个盘子从 中间 柱 移动到 目标 柱
   
   这里你可能会说了，我靠，不是只让移动一个盘子的吗，你这第1步和第3步移动了n-1个盘子啊...，对，所以我这里的过程说的是抽象的过程，也就是说不管具体的实现细节是怎样的，要达成所有的盘子都从A->C的效果，中间一定是有一步是达到这个效果的，就好比你从北京去纽约，假设只有一条国际航班，要经过巴黎，那我就可以说你从北京去纽约，只有两步，第一步是去巴黎，第二步是从巴黎去纽约，这里的道理是同样的。

• 那么现在将上面的第1步怎么实现呢？同样抽象，只要将n 替换成 n-1 即可,第三步也是同理

1. 将n-2个盘子从 起始 柱 移动到 中间 柱
2. 将第n-1个盘子从 起始 柱 移动到 目标 柱
3. 将n-2个盘子从 中间 柱 移动到 目标 柱

代码实现

那这个过程，用程序来抽象就是 一个Plate方法,接受四个参数,n,from,mid,to，四个参数的意思分别是

• n 代表要移动几个盘子
• from 代表起始柱的名字
• mid 代表借助的中间柱的名字
• to 代表目标柱的名字

方法的 作用是 将 n 个盘子 从 from 移动到 to

代码如下

    /**
     * 将n个盘子从 from 移动到 to
     */
    public static void movePlate(int n, String from, String mid, String to) {
        /* 如果只有一个盘子,就直接从 from 移动到 to */
        if (n <= 1) {
            System.out.println(from + " -> " + to);
            return;
        }

        /* 1.将 n-1 个盘子 从 from 移动到 mid */
        movePlate(n - 1, from, to, mid);

        /* 2.将第 n 个盘子 从 from 移动到 to */
        System.out.println(from + " -> " + to);

        /* 3.将 n-1 个盘子 从mid 移动到 to */
        movePlate(n - 1, mid, from, to);
    }

你可以发现除去注释，真正的代码只有5行,就将这个问题给解决了，再次提醒这里的from , mid ,to 是形参，代表的是起始住，中间柱，和目标驻，不是具体的哪一个柱子，所以在第12行，因为第一步是将N-1个移动到中间柱,所以参数时from,to,mid,第18行将n-1个从中间柱移动到目标驻,所以参数时mid,from,to，中间的参数就是需要借助的柱子。

下面测试一下代码,这里根据题目把from,mid,to起个名分别是A,B,C,那执行这个方法就是将3个盘子从A移动到C

    public static void main(String[] args) {
        movePlate(3, "A", "B", "C");
    }

n = 3 的时候

A -> C
A -> B
C -> B
A -> C
B -> A
B -> C
A -> C

Process finished with exit code 0

发现和上面人为思考的结果是一样的哦

当n = 4的时候

A -> B
A -> C
B -> C
A -> B
C -> A
C -> B
A -> B
A -> C
B -> C
B -> A
C -> A
B -> C
A -> B
A -> C
B -> C

Process finished with exit code 0

一共是15步,也没有问题,再多的我就不测了,有兴趣的自己试试按照上面的打印结果来进行操作

推算次数

利用递归的方法同样可以很容易的写出计算次数的方法

    public int countMovePlate(int n) {
        if (n <= 1) return 1;
        return countMovePlate(n - 1) + 1 +countMovePlate(n-1);
    }

那问题来了,还能优化吗？

上文说到人为观察，利用数学归纳法可以得出需要的次数是 \(2^n - 1\) 次，那么这个数究竟是怎么得到呢？

先把上面的程序复制下来，进行观察

        /* 1.将 n-1 个盘子 从 from 移动到 mid */
        movePlate(n - 1, from, to, mid);

        /* 2.将第 n 个盘子 从 from 移动到 to */
        System.out.println(from + " -> " + to);

        /* 3.将 n-1 个盘子 从mid 移动到 to */
        movePlate(n - 1, mid, from, to);

核心代码就三行,假设moveplate这个方法需要移动的次数为\(a_n\)次,那么上面的这三行需要移动的次数就应该是$$ a_n = a_{n-1} + 1 + a_{n-1} $$

第一步是\(a_n\),第二步是固定的1次,第三步又是\(a_n\),然后当 n = 1的时候 \(a_1 = 1\) ，再总结整理一下就成了

\[ a_n=\left\{
\begin{aligned}
1, n = 1\\
2a_{n-1} + 1,n > 1
\end{aligned}
\right.
\]

有没有梦回高中的赶脚，这是一个很简单的变形等比数列，我们让两边都加上1

\[a_n + 1 = 2a_{n-1} + 1 + 1
\]

也就是

\[a_n + 1 = 2a_{n-1} + 2
\]

再提取一下

\[a_n + 1 = 2(a_{n-1} + 1)
\]

两边都除以 \((a_{n-1} + 1)\)

于是就成了

\[\frac {a_n + 1}{a_{n-1} + 1} = 2
\]

那接着将这个公式一直写竖式将他们相乘

\[\frac {a_n + 1} {a_{n-1} + 1} = 2
\]

\[\frac {a_{n-1} + 1}{a_{n-2} + 1} = 2
\]

\[\frac {a_{n-2} + 1}{a_{n-3} + 1} = 2
\]

\[\vdots
\]

\[\frac {a_2 + 1}{a_1 + 1} = 2
\]

接着约分,Markdown LaTex公式的删除线找了半天都没找到，知道的麻烦告知一下.

约分结果是

\[\frac {a_n + 1}{a_1 + 1} = 2^{n-1}
\]

接着将前面的\(a_1 = 1\)代入,于是

\[\frac {a_n + 1}{2} = 2^{n-1}
\]

再整理一下

\[a_n = 2^n - 1 , n > 1
\]

所以说

\[ a_n=\left\{
\begin{aligned}
1, n = 1\\
2^n - 1 , n > 1
\end{aligned}
\right.
\]

将n =1 代入 n > 1 的情况,也是成立的,因此

\[a_n = 2^n - 1
\]

所以经过推导之后java代码如下,因为涉及到\(2^n\)这种运算,可以使用移位符,这样底层移动速度很快

代码如下

    public static int countMovePlate(int n) {
        return n >= 1 ? (1 << n) - 1 : 0;
    }

结论

最终我们解决汉诺塔的移动顺序与统计次数的代码如下,可以看出并不需要几行代码就解决了问题

    /* 打印出移动顺序 */
    public static void movePlate(int n, String from, String mid, String to) {
        if (n <= 1) {
            System.out.println(from + " -> " + to);
            return;
        }
        movePlate(n - 1, from, to, mid);
        System.out.println(from + " -> " + to);
        movePlate(n - 1, mid, from, to);
    }

    /* 返回需要移动的次数 */
    public static int countMovePlate(int n) { return n >= 1 ? (1 << n) - 1 : 0;}