.NetCore下 Exceptionless 分布式日志的个性化处理

Event Type

在Exceptionless中有 Exception 、LogMessage、Broken Links 、Feature Usages

接下来就这几种类型分别添加日志记录

Exception

Exceptionless组件对系统的异常日志都有捕获，所有Exception异常都会添加

当然也可以对异常添加标签

 ex.ToExceptionless().AddTags("tags").Submit();

在Exceptionless站点上可以看到

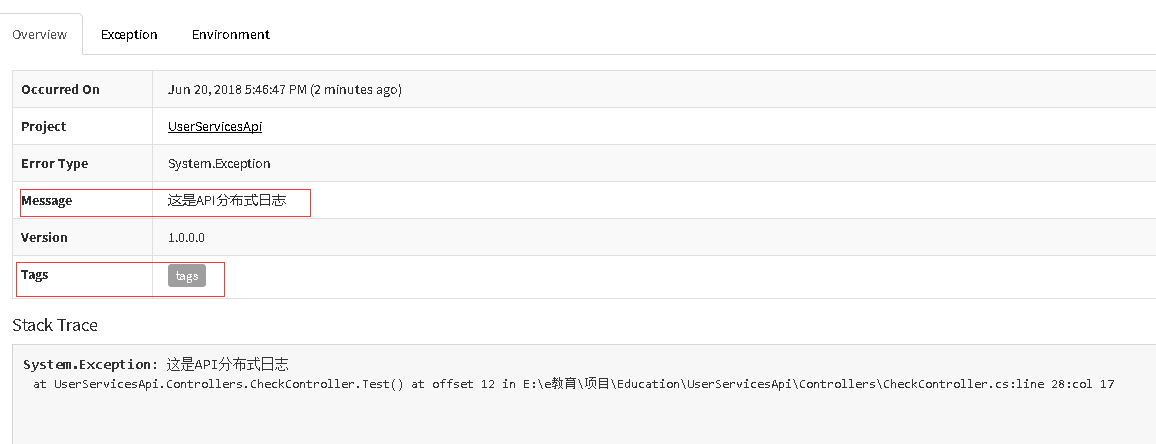
通过详细我们看到tags message

通过这个tags可以查询出对应的日志，方便快速查找

LogMessage

日志信息记录，对于业务需要记录操作日志信息地方可以用如下方式

ExceptionlessClient.Default.CreateLog("LogMessage", ex.Message, LogLevel.Info).AddTags("LogMessage").Submit();

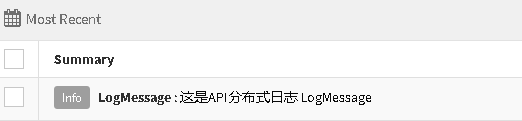
可以设置日志信息 Summary 以及 日志的LogLevel 根据业务需求设置

Broken Links

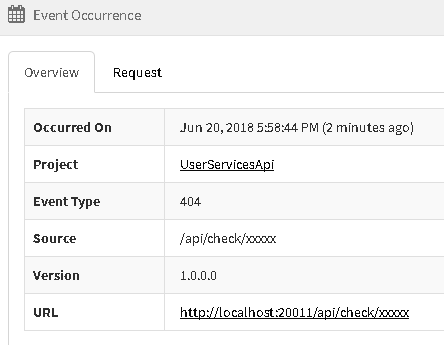
记录404找不到请求的日志

如在地址栏里输入http://localhost:20011/api/check/xxxxx 不存在的地址

可以看到这个日志已经被记录

Feature Usages

ExceptionlessClient.Default.CreateFeatureUsage("custom").SetSource("customsource").SetMessage("这是FeatureUsage日志").SetType("customType").Submit();

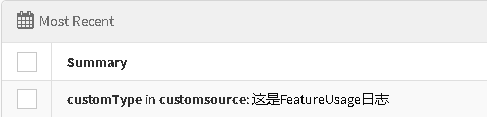
同样添加添加日志的信息、来源、类型、标签等设置，可能不同的exceptionless在语法上有不同