P1036 选数（DFS）

题目 https://www.luogu.org/problemnew/show/P1036

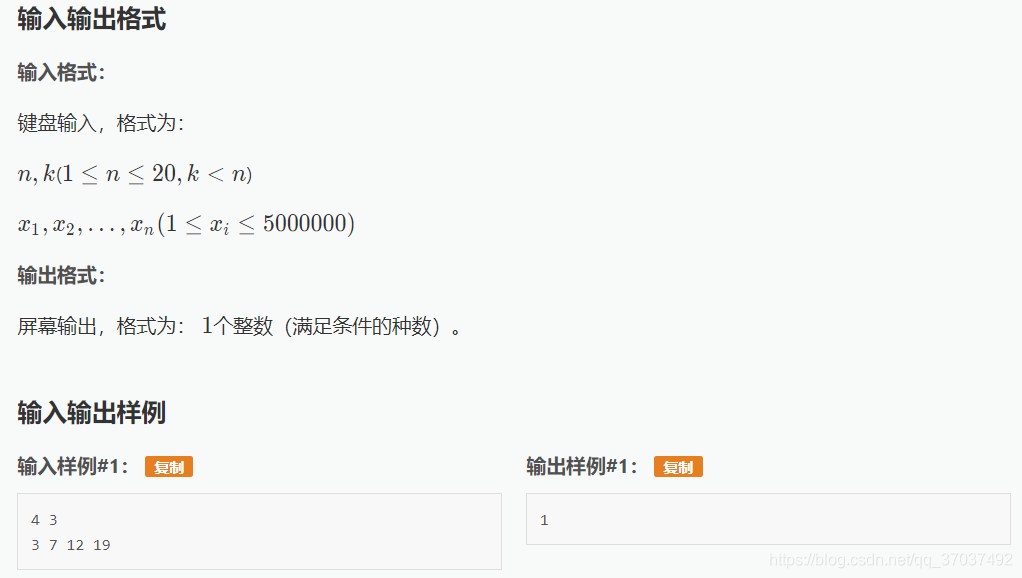
思路

搜索，使用递归实现dfs，所有数字遍历一遍，当取遍所有数组的index（扫了一遍，并非一定是选取了），判断是否取了要求个数的输入和是否是素数

AC代码

#include<cstdio>
#include<cmath>
using namespace std;
int in[22];
int ans=0;
int n, k;
bool isprim(int num) {
    for (int i = 2; i <= sqrt(num); i++)
        if (num % i == 0)
            return false;
    return true;
}
//传递当前选择的数的下标，传递已选择数的个数，以选择的数的总和
void dfs(int cur, int cnt, int num) {
    if (cur == n-1) {
        if (cnt==k&&isprim(num)) {
            ans++;
        }
        return;
    }
    dfs(cur+1,cnt,num);//不拿
    dfs(cur+1,cnt+1,num+in[cur+1]);//拿
}

int main() {
//    freopen("E:\\下载\\testdata (1).in","r",stdin);
    scanf("%d%d", &n, &k);
    for (int i = 0; i <= n-1; i++)
        scanf("%d", &in[i]);
    dfs(-1, 0, 0);
    printf("%d", ans);
    return 0;
}

稍微优化

#include<cstdio>
#include<cmath>

using namespace std;
int in[22];
int ans=0;
int n, k;

bool isprim(int num) {
    for (int i = 2; i <= sqrt(num); i++)
        if (num % i == 0)
            return false;
    return true;
}
//传递当前选择的数的下标，传递已选择数的个数，以选择的数的总和
void dfs(int cur, int cnt, int num) {
    if (cur == n) {
        if (cnt==k&&isprim(num)) {
            ans++;
        }
        return;
    }
    //第一个结点从这开始
    if((k-cnt)>(n-cur))//剩下的不足以满足cnt=k时
        return;
    dfs(cur+1,cnt,num);//不拿
    dfs(cur+1,cnt+1,num+in[cur+1]);//拿
}
int main() {
//    freopen("E:\\下载\\testdata (1).in","r",stdin);
    scanf("%d%d", &n, &k);
    for (int i = 1; i <= n; i++)
        scanf("%d", &in[i]);
    dfs(0, 0, 0);
    printf("%d", ans);
    return 0;
}

我的收获

dfs（）参数可以为index，数量，聚合函数这个样子