51nod 1241 特殊的排序

【题解】　　

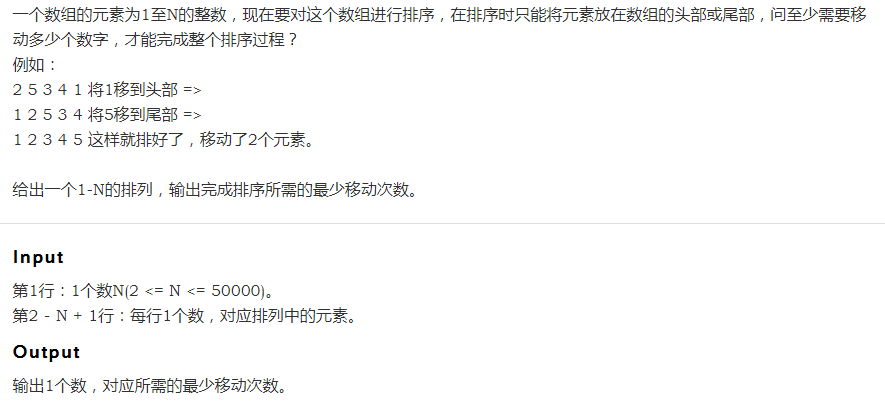
　　设满足前后两个元素之差为1的最长上升子序列LIS的长度为m，那么本题的答案即为n-m.

　　证明：

　　1，n-m次移动一定可以让序列递增。设LIS的第一个数为i，最后一个数为j，我们按照i-1到1的递减的顺序把这些数调换到第一个位置，它们就排好序了。同理处理j+1到n. 总共需要n-m次移动。

　　2，不存在小于n-m次的移动方法。因为如果只需移动k次，k<n-m，那么剩下的n-k个数组成了一个更长的LIS（n-k>m），于LIS的长度为m矛盾。

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #define LL long long
 #define rg register
 #define N 200010
 using namespace std;
 int n,m,ans,a[N],f[N];
 inline int read(){
     int k=,f=; char c=getchar();
     while(c<''||c>'')c=='-'&&(f=-),c=getchar();
     while(''<=c&&c<='')k=k*+c-'',c=getchar();
     return k*f;
 }
 int main(){
     n=read();
     for(rg int i=;i<=n;i++) a[i]=read();
     for(rg int i=;i<=n;i++) f[a[i]]+=f[a[i]-]+,ans=max(ans,f[a[i]]);
 //    printf("%d\n",ans);
 //    for(rg int i=1;i<=n;i++) printf("%d ",f[a[i]]); puts("");
     printf("%d\n",n-ans);
     return ;
 }