hdu 6201 transaction （最短路变形——带负权最长路）

题意：

给定n个城市的货物买卖价格， 然后给定n-1条道路，每条路有不同的路费， 求出从某两个城市买卖一次的最大利润。

利润 = 卖价 - （买价 + 路费）

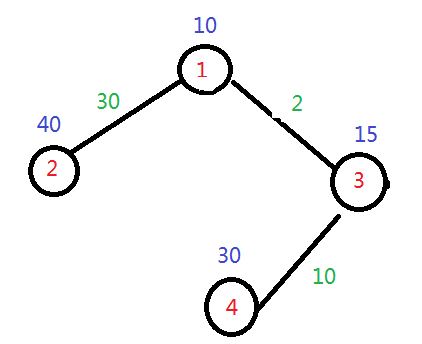
样例数据， 最近是从第一个点买入， 第4个点卖出， 利润为8

分析：

1.如果一条边连接（u，v），路费为cost ，城市买卖价格用P( )表示， 那么他的边权就表达为(P(v) - P(u) - cost).

2.我们可以假设有一个起点。他连接着所有的点，边权为0。

3.那么如果从这个点出发的话， 就等于是把所有的城市都尝试作为买入城市

4.然后只要做一次允许有副权的SPFA最短路算法就能算出正确答案了。

#include <cstdio>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;
const int maxn = 1e5 + ;
int T,n;
int d[maxn], P[maxn], vis[maxn];
struct Node{
    int num;
    int dis;
    Node(int a = , int b = ):num(a), dis(b){}
};
vector<Node> G[maxn];
int spfa(){
    memset(d,-,sizeof(d));//因为要做最长路， 所以把初始值设为-1。
    memset(vis,,sizeof(vis));
    for(int i = ; i <= n; i++) G[].push_back(Node(i,)); // 虚拟一个起点，练向所有的点。
    queue<int> q;

    d[] = ;
    q.push();
    vis[] = ;
    while(!q.empty()){
        int u = q.front();
        for(int i = ; i < G[u].size(); i++){
            int v = G[u][i].num;
            if(d[v] < d[u] + G[u][i].dis){
                d[v] = d[u] + G[u][i].dis;
                if(!vis[v]){
                    q.push(v);
                    vis[v] = ;
                }
            }
        }
        q.pop();
        vis[u] = ;
    }
    int ans = -;
    for(int i = ; i <= n; i++){
        ans = max(ans,d[i]);
    }
//    puts("");
    return ans;
}
void init(int n){
    for(int i = ; i <= n; i++ )
        G[i].clear();
}
int main(){
    scanf("%d", &T);
    while(T--){
        scanf("%d", &n);
        for(int i = ; i <= n; i++){
            scanf("%d", &P[i]);
        }

        for(int i = ; i < n - ; i++){
            int u , v, cost;
            scanf("%d %d %d",&u, &v, &cost);
            G[u].push_back(Node(v,P[v] - P[u] - cost));//双向边
            G[v].push_back(Node(u,P[u] - P[v] - cost));

        }
        printf("%d\n",spfa());
        init(n);//初始化临接表
    }
}