牛顿迭代法（Newton's method）

关键词：牛顿法、牛顿迭代法、牛顿切线法、牛顿-拉弗森方法

参考：牛顿迭代法-百度百科、牛顿切线法-百度文库数学学院、牛顿切线法数值分析、非线性方程（组）的数值解法、Latex入门

https://blog.csdn.net/ccnt_2012/article/details/81837154

一、牛顿切线法基本思想

背景

多数方程不存在求根公式（参考：伽罗瓦理论、一元五次方程求根公式），因此求精确根非常困难，甚至不可能，从而寻找方程的近似根就显得特别重要。方法使用函数的泰勒级数的前面几项来寻找方程的根。牛顿迭代法是求方程根的重要方法之一，其最大优点是在方程的单根附近具有平方收敛，而且该法还可以用来求方程的重根、复根，此时线性收敛，但是可通过一些方法变成超线性收敛。

思路

将非线性方程线性化

设$x_{k}$是$f(x)=0$的近似根，将$f(x)$在$x_{k}$附近用一阶Tylor多项式近似(带皮亚诺余项)：

$$ \begin{align*} f(x)&=f(x_{k})+f'(x_{k})(x-x_{k})+\frac{2f''(ξ)}{2!}(x-x_{k}) \\ &≈f(x_{k})+f'(x_{k})(x-x_{k})+P(x) \end{align*} $$

令$ P(x)=0 $，当$ f'(x)≠0 $时有意义，可用线性方程近似代替

$ f(x)=f(x_{k})+f'(x_{k})(x-f(x_{k})) $

令$ f(x)=0 $，解此线性的方程得：

$x_{k+1} = x_{k}-\frac{f(x_{k})}{f'(x_{k})}$ 　　　

此式即为牛顿迭代公式。

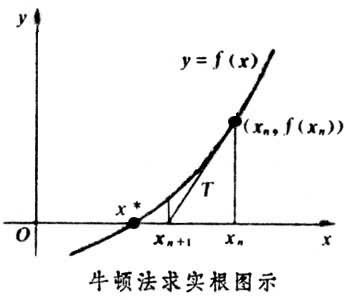
二、牛顿法的几何意义

设一个一元方程：

$$ y = f(x) $$

由图中可看出：

$f(x)=0$ 的根，就是曲线与x轴的交点的横坐标x*。

在曲线上任取一点$(x_{0},f(x_{0}))$，过该点做曲线的切线，其斜率为$f'(x_{0})$，由直线方程$y-y_{0}=k(x-x_{0})$，得到过该点的切线方程：

$$ y=f(x_{0})+f'(x_{0})(x-x_{0}) $$

令$ y=0 $，即$f(x_{0})+f'(x_{0})(x-x_{0}) = 0$，得到该切线与x轴交点的横坐标：

$$ x=x_{0}-\frac{f(x_{0})}{f'(x_{0})} $$

一次迭代后，$ x1=x_{0}-\frac{f(x_{0})}{f'(x_{0})} $

过点$ (x1,f(x1)) $再做曲线的切线，重复以上步骤，切线与x轴交点的横坐标就越来越接近$x^*$。

设$x_{n}$是$x^*$的第$n$次近似值，过$(x_{n},f(x_{n}))$做曲线$y=f(x)$的切线，切线与x轴交点的横坐标为：

$$ x_{n+1} = x_{n}-\frac{f(x_{n})}{f'(x_{n})} $$

因此牛顿法也称牛顿切线法。

三、收敛性与收敛速度

四、应用

1.牛顿迭代法快速寻找平方根

构造方程$f(x)=x^2-n$