洛谷 P1514 引水入城 解题报告

P1514 引水入城

题目描述

在一个遥远的国度，一侧是风景秀美的湖泊，另一侧则是漫无边际的沙漠。该国的行政区划十分特殊，刚好构成一个 NN 行 \times M×M 列的矩形，如上图所示，其中每个格子都代表一座城市，每座城市都有一个海拔高度。

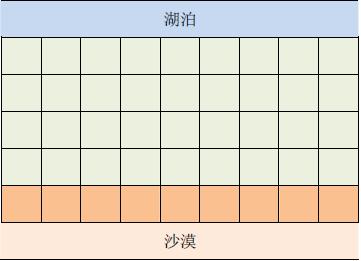
为了使居民们都尽可能饮用到清澈的湖水，现在要在某些城市建造水利设施。水利设施有两种，分别为蓄水厂和输水站。蓄水厂的功能是利用水泵将湖泊中的水抽取到所在城市的蓄水池中。

因此，只有与湖泊毗邻的第 11 行的城市可以建造蓄水厂。而输水站的功能则是通过输水管线利用高度落差，将湖水从高处向低处输送。故一座城市能建造输水站的前提，是存在比它海拔更高且拥有公共边的相邻城市，已经建有水利设施。由于第 NN 行的城市靠近沙漠，是该国的干旱区，所以要求其中的每座城市都建有水利设施。那么，这个要求能否满足呢？如果能，请计算最少建造几个蓄水厂；如果不能，求干旱区中不可能建有水利设施的城市数目。

输入输出格式

输入格式：

每行两个数，之间用一个空格隔开。输入的第一行是两个正整数 N,MN,M ，表示矩形的规模。接下来 NN 行，每行 MM 个正整数，依次代表每座城市的海拔高度。

输出格式：

两行。如果能满足要求，输出的第一行是整数 11 ，第二行是一个整数，代表最少建造几个蓄水厂；如果不能满足要求，输出的第一行是整数 00 ，第二行是一个整数，代表有几座干旱区中的城市不可能建有水利设施。

数据范围：

---

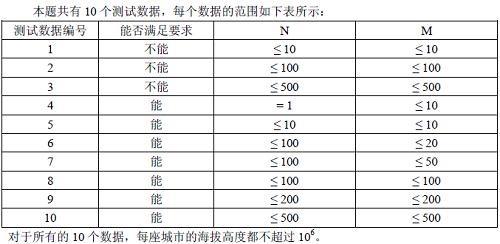
这个题其实是 记忆化搜索+贪心

首先考虑第一行某一个点的贡献，玩一玩我们会发现

如果它对最后一行的贡献不是一段区间，那么就凉了，它覆盖的区间的中间值谁也进不去。

先考虑求出贡献，对每个点进行一次\(dfs\)，通过记忆化不搜索重复的点，即得出了好多个区间

然后判断一下是否有没覆盖的

我们发现，用区间覆盖一个线段是可以贪心的。

以左端点为关键字进行排序。

从左到右对线段进行覆盖。

策略是每次在已经覆盖到的线段中选择一个左端点，要求右端点最远

---

Code:

#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int N=505;
const int X[5]={0,-1,0,1,0};
const int Y[5]={0,0,1,0,-1};
pair <int,int > dx[N];
int vis[N],color[N],used[N][N];//第一排的某些是否访问,最后一排
int ml,mr,n,m,h[N][N],k;
void dfs(int x,int y)
{
    if(used[x][y]) return;
    used[x][y]=1;
    if(x==1)
        vis[y]=1;
    if(x==n)
    {
        color[y]=1;
        mr=max(mr,y);
        ml=min(ml,y);
    }
    for(int i=1;i<=4;i++)
    {
        int tx=x+X[i],ty=y+Y[i];
        if(h[tx][ty]<h[x][y])
            dfs(tx,ty);
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    memset(h,0x3f,sizeof(h));
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            scanf("%d",&h[i][j]);
    for(int i=1;i<=m;i++)
        if(!vis[i])
        {
            memset(used,0,sizeof(used));
            ml=m+1,mr=0;
            dfs(1,i);
            if(ml!=m+1) dx[++k]=make_pair(ml,mr);
        }
    int cnt=0;
    for(int i=1;i<=m;i++)
        if(!color[i])
            cnt++;
    if(cnt)
    {
        printf("0\n%d\n",cnt);
        return 0;
    }
    sort(dx+1,dx+1+k);
    int r=1,i=1,ans=0;
    while(r<=m)
    {
        int mx=0;
        while(dx[i].first<=r)
            mx=max(mx,dx[i++].second);
        r=mx+1;
        ans++;
    }
    printf("1\n%d\n",ans);
    return 0;
}

---

2018.7.25