最大行走路线问题（DP）

在一个NxN的棋盘上，每个格子里有若干个棋子，假设起点为左上角的格子，且每次只能向下或向右走一格，问怎样走才能得到最多的棋子。

这是很简单的递推题了。

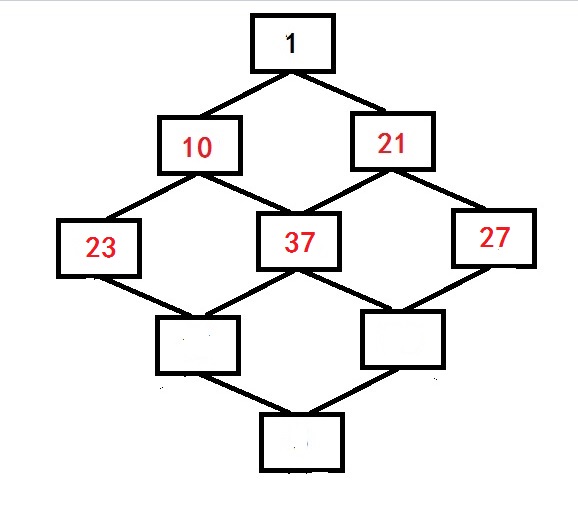
因为只能向下或者向右，所以其实我们可以把棋盘看成一颗这样的树（以N=3为例）

起点最上，终点最下，数字即为棋子，只能向下走，要找一条数字总和最大的路线。

这个问题怎么考虑呢，我们可以从头开始推，然后记录起始点到其他所有点的最大值。

先保存第一行到第二行的最大值　　　　　　　　　　　　　　                               再保存第三行，这时中间的有两条路，选择最大那条即可

                              

由此就可得到起始点到任意点的最大距离

由此我们可以知道，从下往上，每个点都是选择上面连接的两个点中，距离最大的那个，然后加上自身的值。

设map[n][n]保存棋盘每个点的棋子数，dp[n][n]保存起始点到每个点的最大距离

即有状态转移方程：

dp[i][j] = dp[i][j-1] + dp[i-1][j] + map[i][j]

#include <iostream>
#include <string>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <stack>
using namespace std;

#define MEM(a,b) memset(a,b,sizeof(a))
#define pf printf
#define sf scanf
#define debug printf("!/m")
#define INF 1000
#define MAX(a,b) a>b?a:b
#define blank pf("\n")
#define LL long long

LL dp[INF][INF];

LL map[INF][INF];

typedef pair<int,int> pa;

stack<pair<int,int> > road;

int main()
{
          int n,i,j;

          MEM(map,);
          MEM(dp,);;

          pf("请输入棋盘的维度n\n");
          sf("%d",&n);

          pf("请输入棋盘每个格子里的棋子数\n");
          for(i = ;i<=n;i++)
          {
                    for(j = ;j<=n;j++)
                    {
                              sf("%lld",&map[i][j]);
                    }
          }

          for(i = ;i<=n;i++)
          {
                    for(j = ;j<=n;j++)
                    {
                              dp[i][j] = max(dp[i-][j],dp[i][j-]) + map[i][j];
                    }
          }

          road.push(make_pair(n,n));
          int a=n,b=n;
          for(;;)
          {
                    if(dp[a][b-] >= dp[a-][b])
                              b = b-;
                    else
                              a = a-;
                    if(a== || b==)
                              break;
                    road.push(make_pair(a,b));
          }

          pf("起始点到每个点的最大距离如下\n");
          for(i = ;i<=n;i++)
          {
                    for(j = ;j<=n;j++)
                    {
                              pf("%lld\t",dp[i][j]);
                    }
                    blank;
          }

          pf("得到的最多的棋子为%lld\n",dp[n][n]);

          pf("路径如下:\n");
          while(!road.empty())
          {
                    pa x= road.top();
                    road.pop();
                    pf("(%d,%d) ",x.first,x.second);
          }
          blank;

    return ;
}
/*
3
1 20 6
9 16 19
13 15 5
*/