webgl 背面剔除
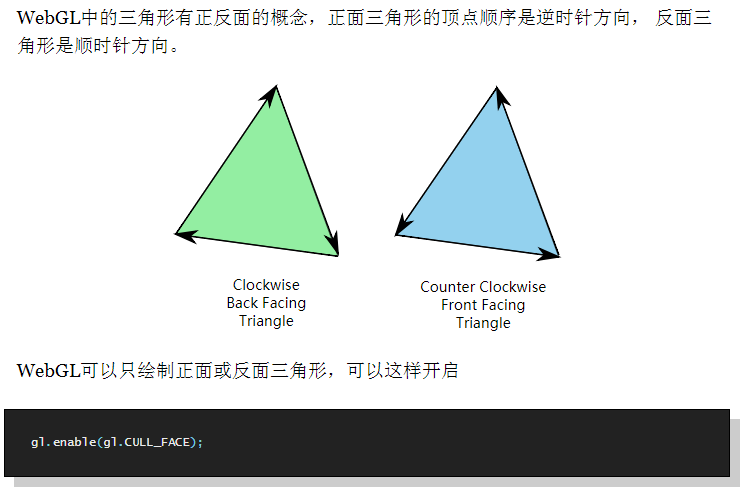
webgl 背面剔除的更多相关文章
- OPENGL——背面剔除
Opengl 表面剔除是提高 Opengl 程序渲染效率的一个有效途径. 我们知道,OpenGL 渲染的基本单位是一个个的三角形面片.无论多么复杂的3D 模 型都是由一个个基本的三角型的面片组成的. ...
- OpenGL 背面剔除
在OpenGL种可使用glEnable(GL_CULL_FACE)开启背面剔除功能,即把那些我们看不见的面删除.但在剔除之前我们需要定义正面和背面,这个可以用法线来理解.在数学学科中,法线是用右手法则 ...
- OpenGL学习脚印:背面剔除(Face Culling)
写在前面 在绘制封闭类型的几何对象时,开启背面剔除功能能够提高渲染性能.本节简要介绍下背面剔除,示例程序可以在我的github下载. 什么是背面剔除 当我们观察场景中对象时,一般只能以一定角度来观察, ...
- WEBGL学习【八】模型视图投影矩阵
<!--探讨WEBGL中不同图形的绘制方法:[待测试2017.11.6]--> <!DOCTYPE HTML> <html lang="en"> ...
- WEBGL学习【七】画布绘图
主要是对WEBGL的绘图部分进行了进一步加强的认识和理解 <!DOCTYPE HTML> <html lang="en"> <head> < ...
- WebGL学习笔记(四):绘图
图元 WebGL可以绘制非常复杂的3D模型,这些模型都是由下面3种基本几何图元构成的,下面我们来详细的看看. 三角形 WebGL中任何复杂的模型,都是由三角形组合而成的,可以说三角形是任意形状的最小构 ...
- WebGL学习笔记(一):理解基本概念和渲染管线
WebGL 是以 OpenGL ES 2.0 为基础的 3D 编程应用接口. 渲染管线(图形流水线) 渲染管线是指将数据从3D场景转换成2D图像,最终在屏幕上显示出来的总过程.它分为几个阶段:应用阶段 ...
- WebGL 渲染管线
WebGL 是以 OpenGL ES 2.0 为基础的 3D 编程应用接口. WebGL依赖GPU的图形渲染能力,即依赖硬件设备,所以其渲染流程和GPU内部的渲染管线是相符的.渲染管线的作用是将3D模 ...
- WebGL之绘制三维地球
通过Three.js也许可以很方便的展示出3D模型,但是你知道它是怎么一步一步从构建网格到贴图到最终渲染出3D模型的吗?现在我们直接使用底层的webgl加上一点点的数学知识就可以实现它. 本节实现的效 ...
随机推荐
- hash环/consistent hashing一致性哈希算法
一致性哈希算法在1997年由麻省理工学院提出的一种分布式哈希(DHT)实现算法,设计目标是为了解决因特网中的热点(Hot spot)问题,初衷和CARP十分类似.一致性哈希修正了CARP使用的 ...
- 20155218 《Java程序设计》实验五(网络编程与安全)实验报告
20155218 <Java程序设计>实验五(网络编程与安全)实验报告 一.实验内容及步骤 (一) 编写MyBC.java实现中缀表达式转后缀表达式的功能 编写MyDC.java实现从上面 ...
- MYSQL中日期与字符串间的相互转换
一.字符串转日期 下面将讲述如何在MYSQL中把一个字符串转换成日期: 背景:rq字段信息为:20100901 1.无需转换的: SELECT * FROM tairlist_day WHERE rq ...
- springmvc 使用 response 的注意事项以及解决500 空指针异常找不到 response 的方法
使用注解方式在类中(Controller)来装载request时,是可以正常使用request的(必须在启动时才注入,所以不支持热部署),但是同样使用这种方式在已经装载了 request的情况下装载 ...
- SOAPUI参数中xml中CDATA包含问题
<