深入解析d3弦图

记得上次看d3应该是1年前的事情了，当时还一边看一边写了d3(v5.7)的一个学习笔记：https://www.cnblogs.com/eco-just/tag/d3/

后来转战three.js就没继续研究了(其实也是感觉api层面的东西也没有深入研究的必要，何况后续项目也不会用到这些东西)。

期间也有同行通过博客问过弦图的问题，出于种种原因吧，当时并没有深入研究。

但是今天！我们就结合d3的3.5.16版本来深入解析一下d3的弦图吧。（demo是找的简书上这为同学的笔记：https://www.jianshu.com/p/4b44c708c2da）

先上效果：

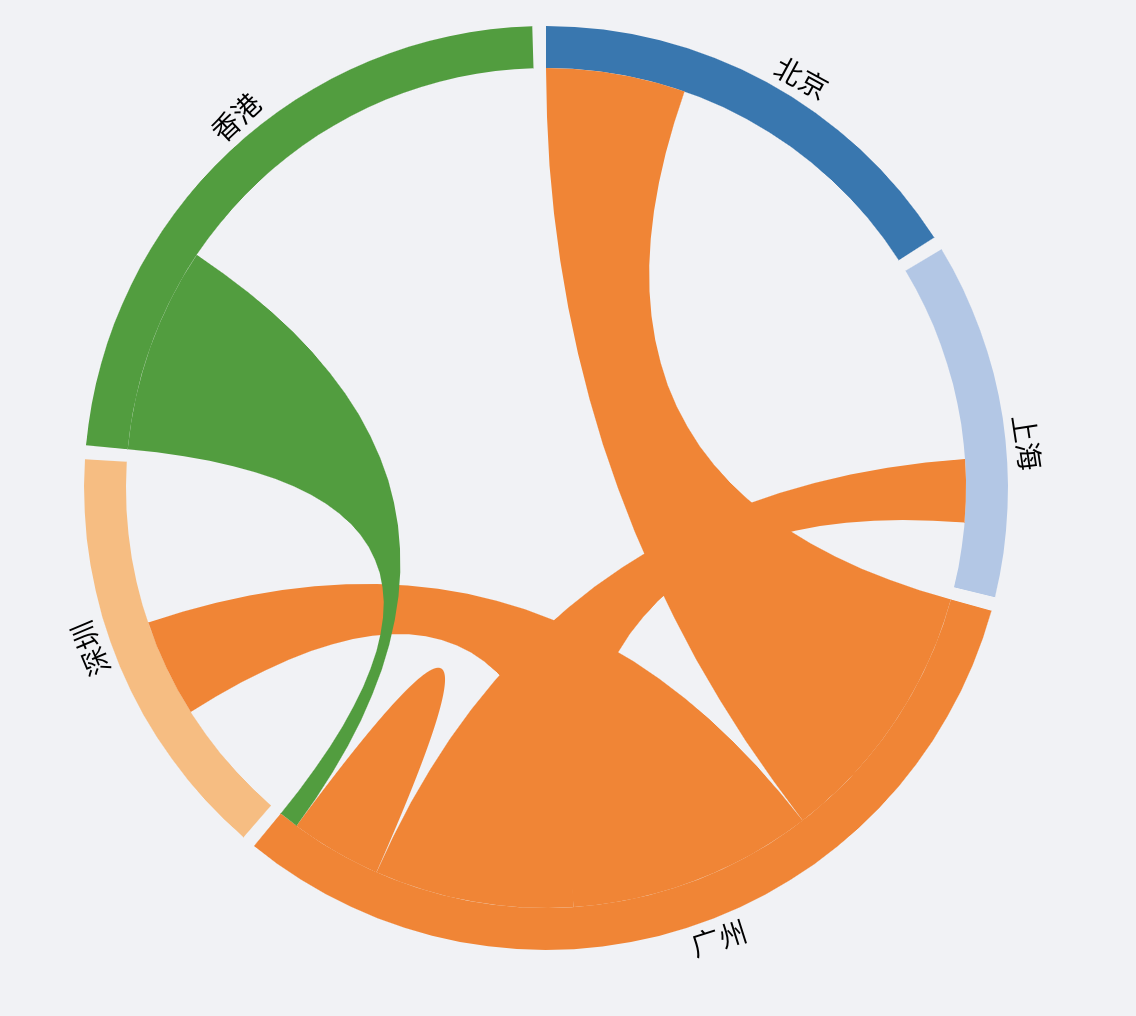
step1:根据数据初始化布局

code:

// 初始数据
    var city_name = [ "北京" , "上海" , "广州" , "深圳" , "香港"  ];
    var population = [
              [ ,   ,  ,  ,  ],
              [ ,   ,  ,   ,  ],
              [ ,   ,  ,  ,   ],
              [ ,   ,  ,  ,  ],
              [ ,   ,  ,  ,  ]
            ];
 
    // 弦布局初始化
    var chord_layout = d3.layout.chord()
                            .padding(0.03)
                            .sortSubgroups(d3.descending)
                            .matrix(population);
 
    // 获取弦布局初始化后的数据
    var groups = chord_layout.groups();
    var chords = chord_layout.chords();

解析：

population数据表格化

	北京	上海	广州	深圳	香港
北京	1000	3045	4567	1234	3714
上海	3214	2000	2060	124	3234
广州	8761	6545	3000	8045	647
深圳	3211	1067	3214	4000	1006
香港	2146	1034	6745	4764	5000

先用d3.layout.chord()这个api传入数据，初始化布局所需要的数据groups、chords；

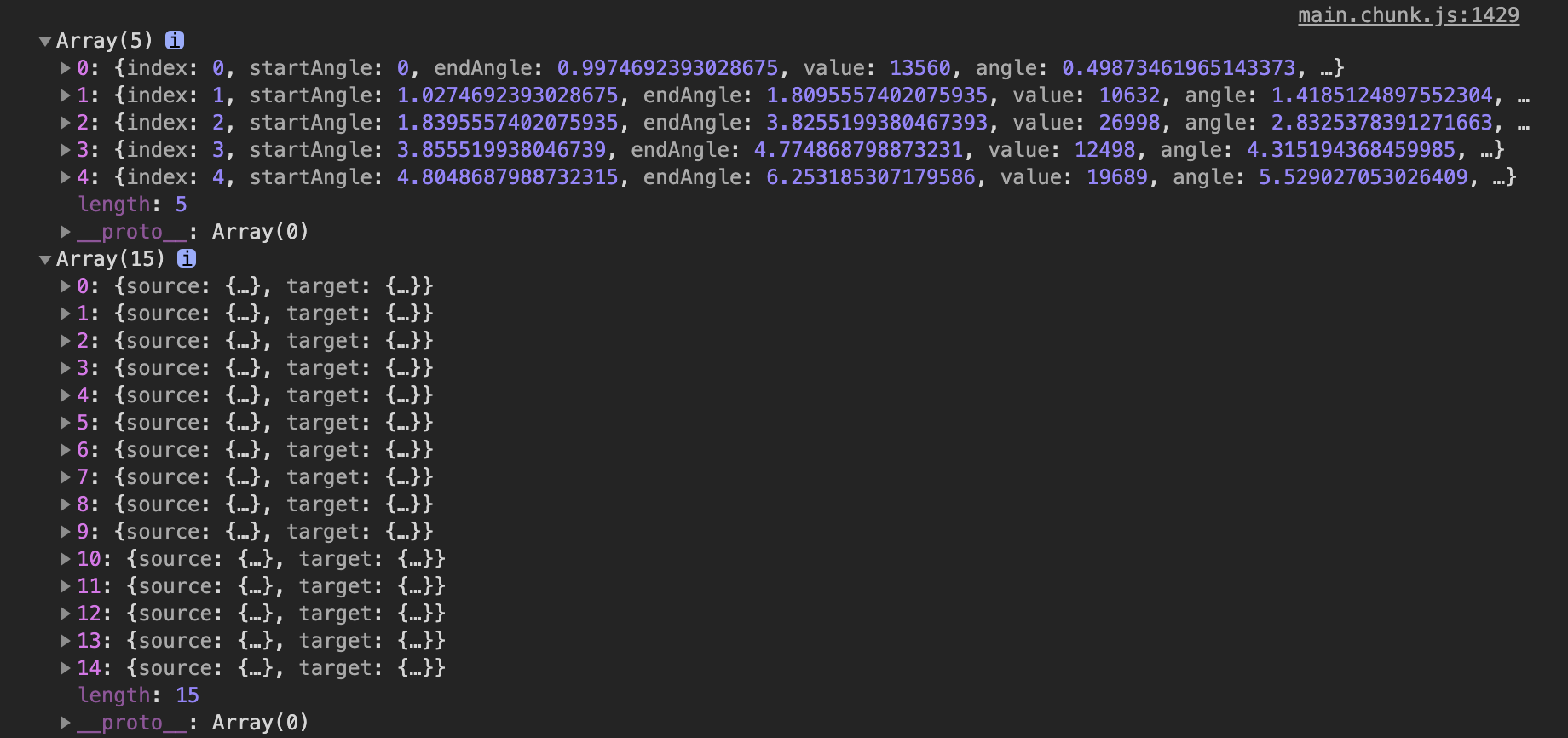
groups数据5条，5个城市，根据population所占权重分配圆弧的大小，在上述数据上的反应就是startAngle和endAngle；

chords数据15条，5个城市选两个(source,target)，根据排列组合应该是5+4+3+2+1=15种(source,target可以相同)；

step2:绘制画布和计算内外圆半径

// svg画布
    var width = ;
    var height = ;
    var svg = d3.select(".d3content")
                .append("svg")
                .attr("width",width)
                .attr('height', height)
                .append("g")
                .attr('transform', 'translate(' + width/ + "," + height/ + ")");
 
    var color20 = d3.scale.category20();
 
    var innerRadius = width/ * 0.7;
    var outerRadius = innerRadius * 1.1;

解析：

.d3content是画布依赖的根元素dom，上述代码将会在600X600的画布上绘制接下来的弦图；

step3:绘制外圆和文字

    var outer_arc = d3.svg.arc()
                        .innerRadius(innerRadius)
                        .outerRadius(outerRadius);
    //绘制外圆（5个城市）
    var g_outer = svg.append("g");
    g_outer.selectAll("path")
            .data(groups)
            .enter()
            .append("path")
            .style("fill",function(d) {
                return color20(d.index);
            })
            .style("stroke",function(d) {
                color20(d.index);
            })
            .attr("d",outer_arc)   // 此处调用了弧生成器
            ;
　　//绘制文字
    g_outer.selectAll("text")
            .data(groups)
            .enter()
            .append("text")
            .each(function(d,i) {   // 对每个绑定的数据添加两个变量
                d.angle = (d.startAngle +　d.endAngle) / ;
                d.name = city_name[i];
            })
            .attr("dy",".35em")
            .attr('transform', function(d) {    // 平移属性
                var result =  "rotate(" +　(d.angle*/Math.PI) + ")";
                result += "translate(0," + - * (outerRadius + ) + ")";
                if (d.angle > Math.PI *  /  && d.angle < Math.PI *  /  )
                    result += "rotate(180)";
                return result;
            })
            .text(function(d) {
                return d.name;
            });

效果图：

注意上述有一句代码：

.attr("d",outer_arc)   // 此处调用了弧生成器

对于每个path都会根据这个函数来绘制，而这个函数对于对应源码里的d3.svg.arc，并且这里有个隐藏的东西：

.attr("d",out_arc)，第二个参数执行的时候(他是一个函数)，会将数据作为实参传给他，于是到了源码里：

d3.svg.arc = function() {
    var innerRadius = d3_svg_arcInnerRadius,
 　　　　outerRadius = d3_svg_arcOuterRadius,
　　　　 cornerRadius = d3_zero,
　　　　 padRadius = d3_svg_arcAuto,
　　　　 startAngle = d3_svg_arcStartAngle,
　　　　 endAngle = d3_svg_arcEndAngle,
　　　　 padAngle = d3_svg_arcPadAngle;
    function arc() {
      var r0 = Math.max(, +innerRadius.apply(this, arguments)),
　　　　　　r1 = Math.max(, +outerRadius.apply(this, arguments)),
　　　　　　a0 = startAngle.apply(this, arguments) - halfπ,
　　　　　　a1 = endAngle.apply(this, arguments) - halfπ,
　　　　　　da = Math.abs(a1 - a0), 
　　　　　　cw = a0 > a1 ?  : ;
      if (r1 < r0) rc = r1, r1 = r0, r0 = rc;
      if (da >= τε) return circleSegment(r1, cw) + (r0 ? circleSegment(r0,  - cw) : "") + "Z";
      var rc, cr, rp, ap, p0 = , p1 = , x0, y0, x1, y1, x2, y2, x3, y3, path = [];
　　.....
}

这个arguments就是如下这样的单条数据：

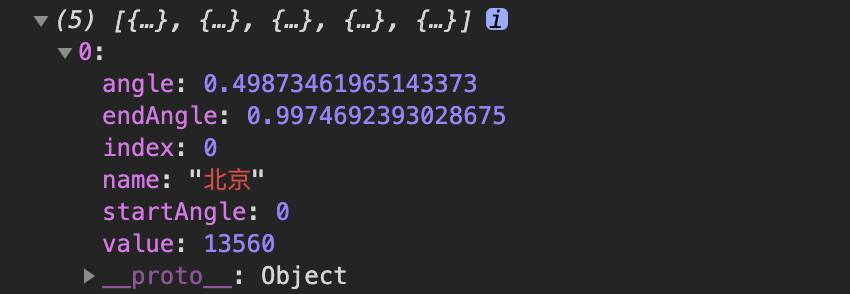
最终根据传入的数据，加上一系列的逻辑处理返回了一个path节点的d属性值，具体的判断逻辑，我截图一张供各位欣赏，如果你有兴趣可以逐个去找他的函数：

最后，由这个属性值绘制了一个path节点：

后面的绘制文字就不多说了，注意一点，回调函数形参里面的d是data(数据)的意思，i是index(索引)的意思。

step4：绘制内弦chord

    // 弦生成器
    var inner_chord = d3.svg.chord()
                            .radius(innerRadius);
                            console.log(inner_chord)
 
    // 添加g元素，接下来在这个元素里面绘制chord
    var g_inner = svg.append("g")
                    .attr("class","chord");
 
    g_inner.selectAll("path")
            .data(chords)
            .enter()
            .append("path")
            .attr("d",inner_chord)  // 调用弦的路径值
            .style("fill",function(d,i) {
                return color20(d.source.index);
            })
            .style("opacity",)
            ;

为了大家看得清晰，我把之前绘制的外圆注释了：

解析：

同理，这里通过d3.svg.chord来绘制弦，依据的数据是：

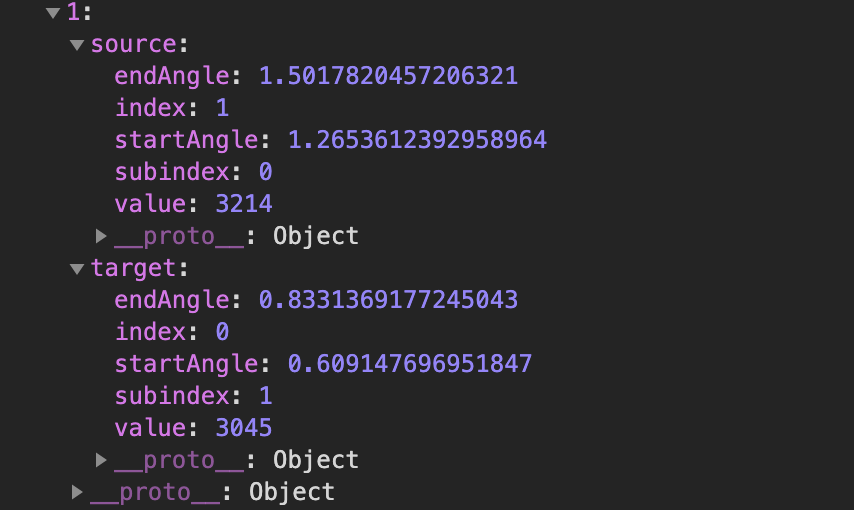
同样贴上源码的主要部分：

d3.svg.chord = function() {
    var source = d3_source,
　　　　 target = d3_target,
　　　　 radius = d3_svg_chordRadius,
　　　　 startAngle = d3_svg_arcStartAngle,
　　　　 endAngle = d3_svg_arcEndAngle;
    function chord(d, i) {
      var s = subgroup(this, source, d, i),
　　　　　　t = subgroup(this, target, d, i);
      return "M" + s.p0 + arc(s.r, s.p1, s.a1 - s.a0) + (equals(s, t) ? curve(s.r, s.p1, s.r, s.p0) : curve(s.r, s.p1, t.r, t.p0) + arc(t.r, t.p1, t.a1 - t.a0) + curve(t.r, t.p1, s.r, s.p0)) + "Z";
    }

equals(s,t)判断两个端点是否相同来决定绘制的方式；

我们看到这里绘制路径，主要用到了两个函数arc()和curve()；

　　 function arc(r, p, a) {
      return "A" + r + "," + r + " 0 " + +(a > π) + ",1 " + p;
    }
    function curve(r0, p0, r1, p1) {
      return "Q 0,0 " + p1;
    }

关于svg的path绘制中各参数的含义，下面给一张图，这里就不多说了：

所以弦主要就是由svg内置的弧绘制api来绘制的(普通的弧线/贝塞尔曲线)！