CF444A DZY Loves Physics【结论】

题目传送门

话说这道题不分析样例实在是太亏了...结论题啊...

但是话说回来不知道它是结论题的时候会不会想到猜结论呢...毕竟样例一、二都有些特殊。

观察样例发现选中的子图都只有一条边。

于是猜只有一条边的时候解最优。

飞快地写个暴力，然后和结论对拍，然后假装这个结论是对的，然后就$AC$了（大雾

还是证明一下这个结论吧：

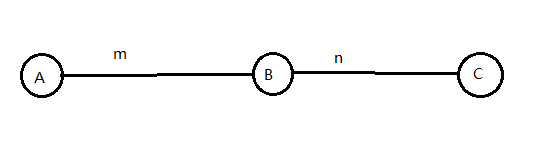
用反证法。

设这样三个点的点权分别为$A$,$B$,$C$，两条边的边权为$n$,$m$

假设子图中有$A,B,C$三个点比只有两个点更优。

也就是三个点都选的答案比只选$AB$和只选$BC$都大。

三个都选的答案：$(A+B+C)/(n+m)$

只选$AB$:$(A+B)/m$

只选$BC$:$(B+C)/n$

则：

$$(A+B+C)/(n+m)>(A+B)/m$$

$$(A+B+C)/(n+m)>(B+C)/n$$

化简：（权都是正数）

$$(A+B+C)*m>(A+B)*(n+m)$$

$$(A+B+C)*n>(B+C)*(n+m)$$

$$↓$$

$$C*m>A*n+B*n$$

$$A*n>B*m+C*m$$

相加：
$$C*m+A*n>A*n+B*n+B*m+C*m$$

$0>B*n+B*m$

由于$B$和$n$,$m$都是正数，导出矛盾。

所以假设不成立。

另外，如果$AC$之间有连边的话，那三个都选肯定更不优，分子不变，分母变大了嘛。只选$AC$都不用讨论，至少在这种情况下三个都选干不过只选$AB$或$BC$。

暴力程序（拿来对拍）

有同学写的$2^n$枚举子集的暴力，我觉得略麻烦，还是更喜欢自己的（笑）

甚至还想优化一下自己的暴力，就是在以$1$以外的点为起点的时候，就不把$1$加进去，因为$1$有的状态已经在$1$为起点的算过了。

但是反正是拿来写对拍嘛，节约考试时间。

 #include<cstdio>
 #include<algorithm>
 #include<vector>
 #include<queue>
 using namespace std;
 #define N 505
 #define ll long long
 int n,m;
 int a[N];
 bool vis[N];
 double ans=0.0;
 vector<pair<int,int> >G[N];
 int rd()
 {
     int f=,x=;char c=getchar();
     while(c<''||c>''){if(c=='-')f=-; c=getchar();}
     while(c>=''&&c<=''){x=(x<<)+(x<<)+(c^);c=getchar();}
     return f*x;
 }
 void dfs(int u,int d,int b)
 {
     for(int i=;i<G[u].size();i++)
     {
         int v=G[u][i].first;
         if(vis[v]) continue;
         vis[v]=;
         int tmp=;
         for(int j=;j<G[v].size();j++)
             if(vis[G[v][j].first]) tmp+=G[v][j].second;
         dfs(v,d+a[v],b+tmp);
         vis[v]=;
     }
     if(b==) return ;
     ans=max(ans,1.0*d/b);
 }
 int main()
 {
     n=rd(),m=rd();
     for(int i=;i<=n;i++)
         a[i]=rd();
     for(int i=;i<=m;i++)
     {
         int u=rd(),v=rd(),w=rd();
         G[u].push_back(make_pair(v,w));
         G[v].push_back(make_pair(u,w));
     }
     for(int i=;i<=n;i++)
     {
         vis[i]=;
         dfs(i,a[i],);
         vis[i]=;
     }
     printf("%.9f\n",ans);
     return ;
 }
 //不分析样例真的是个不好的习惯啊 

Code

正解程序：（比暴力好写）

 #include<cstdio>
 #include<algorithm>
 #include<vector>
 #include<queue>
 using namespace std;
 #define N 505
 #define ll long long
 int n,m;
 int a[N];
 double ans=0.0;
 int rd()
 {
     int f=,x=;char c=getchar();
     while(c<''||c>''){if(c=='-')f=-; c=getchar();}
     while(c>=''&&c<=''){x=(x<<)+(x<<)+(c^);c=getchar();}
     return f*x;
 }
 int main()
 {
     n=rd(),m=rd();
     for(int i=;i<=n;i++)
         a[i]=rd();
     for(int i=;i<=m;i++)
     {
         int u=rd(),v=rd(),w=rd();
         ans=max(ans,1.0*(a[u]+a[v])/w);
     }
     printf("%.9f\n",ans);
     return ;
 }

Code