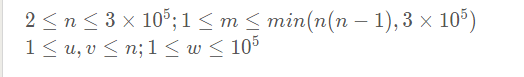$SCOJ4427 Miss Zhao's Graph$
\(problem\)
给定一个包含n个顶点m条边的带权有向图,找一条边数最多的路径,且路径上的边的权值严格递增。
图中可能有重边和自环。
\(题意非常简单:n个点 m个带权边 最多能连成多少条边\)
\(看起来像搜索 就拿搜索水了一波\)
\(然后吧评测都卡爆了(而且只有9pts)\)
总是觉得好亏
\(打了一只前向星+DFS瞎搜\)(大雾)
\(~~恶心的DP题~~\)
\(9pts -> 0pts -> 64pts -> 73pts - >91pts ->100pts\)
数据范围很大 显然\(O(N)\) \(or\) $O(M) $
这题用搜索可以达到 \(O(N*玄学)\) 玄学 = 一次搜索时间 >\(如果带上记忆化 应该快点\)
\(那么DP的解法是O(M)的 每条边跑一次 记录一次\)
重点 ->“递增”
首先 要按权值给边排序
\(所以 应该注重权值相同的边\)
\(if(i < m and edge[i].dis == edge[i+1].dis) continue ;\)
\(加不加等于都没有关系 因为初始值是0\)
\(权值相同就直接跳过 否则会Wrong Answer\)
\(这是特判权值相同的边\)
cnt数组用来储存边权相同的情况
这句\(cnt[edge[k].to] = max ( cnt[edge[k].to] , dp[edge[k].from] + 1 ) ;\) 不要手欠把dp和cnt打错 否则喜提WA数量不等(滑稽
还有一句话 \(十年OI一场空 不开LL见祖宗orz\)
实测int WA了一个点
\(code\)
#include <bits/stdc++.h>
using namespace std;
typedef long long LL ;
inline LL In() { LL res(0),f(1); register char c = getchar() ;
while(!isdigit(c)) { if(c == '-') f = -1 ; c = getchar() ; }
while(isdigit(c)) res = (res << 1) + (res << 3) + (c & 15) , c = getchar() ; return res * f ;
}
int n , m ;
const int N = 300000 ;
struct node{
int from ;
int to ;
int dis ;
}edge[N] ;
LL cnt[N] ;
LL dp[N] ;
bool cmp(node x,node y) { return x.dis < y.dis ; }
signed main() {
memset(edge,0,sizeof(edge)) ; memset(dp,0,sizeof(dp)) ;
n = In() ; m = In() ;
for(register int i =1 ; i <= m ; i ++) {//读入
int u = In() , v = In() , w = In() ;
edge[i] = (node){u,v,w} ;
}
sort(edge+1 , edge+m+1 , cmp) ;//排序
int pos = 1 ;
for(register int i = 1 ;i <= m ;i ++) {//DP
if(i < m and edge[i].dis == edge[i+1].dis) continue ;//特判权值相同
for(register int k = pos ; k <= i ; k ++) cnt[edge[k].to] = max ( cnt[edge[k].to] , dp[edge[k].from] + 1 ) ;
for(register int k = pos ; k <= i ; k ++) dp[edge[k].to] = cnt[edge[k].to] ;
pos = i + 1 ;
}
cout << * max_element( dp + 1 , dp + n + 1 ) << endl ;//最大值函数
return 0;
}

随机推荐
- 用户态文件系统fuse学习【转】
本文转载自:https://blog.csdn.net/ty_laurel/article/details/51685193 FUSE概述 FUSE(用户态文件系统)是一个实现在用户空间的文件系统框架 ...
- POJ 1330 Nearest Common Ancestors 【最近公共祖先LCA算法+Tarjan离线算法】
Nearest Common Ancestors Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 20715 Accept ...
- python列表切片
Python中符合序列的有序序列都支持切片(slice),例如列表,字符串,元组. 格式:[start:end:step] start:起始索引,从0开始,-1表示结束 end:结束索引 step:步 ...
- sqlite:多线程操作数据库“database is locked”解决方法
1. 使sqlite支持多线程(不确定是否非加不可,暂且加上,以备后患) 可以在编译时/启动时/运行时选择线程模式,参考:http://www.cnblogs.com/liaj/p/4015219.h ...
- 「SDOI 2009」Elaxia的路线
发现自己这几天智商完全不在线-- 这道题的数据十分的水,怎样都可以艹过去-- 开始想了一个完全错误的算法,枚举一对点,判断这一对点是否同时在两条最短路上,是就用两点之间的路径更新答案.显然这样是错的: ...
- C#多线程编程介绍——使用thread、threadpool、timer
C#多线程编程介绍——使用thread.threadpool.timer 在system.threading 命名空间提供一些使得能进行多线程编程的类和接口,其中线程的创建有以下三种方法:thread ...
- python-多线程3-生产者消费者
'''生产者和消费者''' ''' 用python写一个多线程的生产者和消费者 生产者x x>0,有东西,print(不生产) x=0,没东西,print(生产) for循环 消费者x x=0, ...
- 「LOJ#10042」「一本通 2.1 练习 8」收集雪花 (map
题目描述 不同的雪花往往有不同的形状.在北方的同学想将雪花收集起来,作为礼物送给在南方的同学们.一共有 n 个时刻,给出每个时刻下落雪花的形状,用不同的整数表示不同的形状.在收集的过程中,同学们不希望 ...
- ACM学习历程—HDU5418 Victor and World(动态规划 && 状压)
这个题目由于只有16个城市,很容易想到去用状压来保存状态. p[i][state]表示到i城市经过state状态的城市的最优值(state的二进制位每一位为1表示经过了该城市,否则没经过) 这样p[j ...
- 京东SDK模板卡盘效果实现代码
最近在做京东模板,因为是最新平台,好多功能都需要摸索,俺技术一般,摸索出一个简易的卡盘功能 ——————使用的是分类推荐模块哦! 本着共享的精神,俺将代码放到这儿了,各人请自便.(代码还不够完善, ...