负样本采样及bias校准、ctr平滑

参考：https://zhuanlan.zhihu.com/p/31529643

在CTR预估中，负样本采样是一种常见的特征工程方法。一般CTR预估的原始正负样本比可能达到1:1000~1:10000左右，而要获取好的效果，一般需要采样到1:5~1:15之间（VC维可推导）。

我们详细分析采样对于pCTR的影响。

设采样前CTR为  ,采样后CTR为  ,正样本数为  ,负样本数为  ,正样本采样概率为  ,负样本采样概率为 ，其中 $n=m/l$。

$ p = \frac{a}{a + b}$

$p' = \frac{la}{la + mb} = \frac{a}{(a + nb)} $

两者化简得到：$p = \frac{p'}{p' + (1 - p') / n}$

注意 $p$为我们希望得到的校准后概率；但由于我们用采样的数据进行训练，模型计算出的pCTR实际为校准前概率$p'$ 。

可以看到，负采样之后的pCTR值会被高估【$p' + (1-p')/n > 1$】。这对于一般的CTR排序影响不大，但对于DSP这类有强烈的保距需求的场景，需要将pCTR校准回对采样前的估计。

对于LR、FM等用logistics function做处理的模型，可以得到

$p' = \frac{p}{n + p -np} = \frac{1}{1 + e^{-(w^Tx + b)}}$

两者化简可得

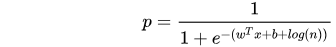
因此可以计算出校准后的bias: $b' = b + log(n)$

---

参考： http://d0evi1.com/ctr-smooth/    http://www.flickering.cn/%E6%95%B0%E5%AD%A6%E4%B9%8B%E7%BE%8E/2014/06/lda%E6%95%B0%E5%AD%A6%E5%85%AB%E5%8D%A6%E8%AE%A4%E8%AF%86betadirichlet%E5%88%86%E5%B8%83/

伯努利试验（Bernoulli experiment）是在同样的条件下重复地、相互独立地进行的一种随机试验，其特点是该随机试验只有两种可能结果：发生或者不发生。

二项分布：重复n次独立的伯努利试验。在每次试验中只有两种可能的结果，而且两种结果发生与否互相对立，并且相互独立，与其它各次试验结果无关，事件发生与否的概率在每一次独立试验中都保持不变，则这一系列试验总称为n重伯努利实验，当试验次数为1时，二项分布服从0-1分布。

二项分布概率：

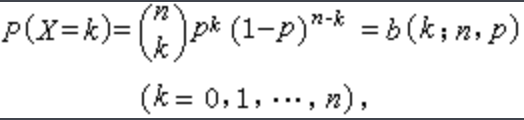
beta分布：beta分布可以看作一个概率的概率分布，当你不知道一个东西的具体概率是多少时，它可以给出了所有概率出现的可能性大小。beta分布的定义域是(0,1)，与概率的范围是一致的。它有两个正值参数，称为形状参数，一般用$\alpha$ 和 $\beta$表示。

Beta分布的均值是：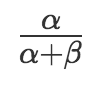

方差是：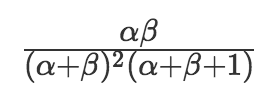

https://jiayi797.github.io/2017/07/09/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0%E5%AE%9E%E8%B7%B5-%E8%BD%AC%E5%8C%96%E7%8E%87%E9%A2%84%E4%BC%B0%E4%B9%8B%E8%B4%9D%E5%8F%B6%E6%96%AF%E5%B9%B3%E6%BB%91/

以后再看吧～～～