Tarjan算法 详解+心得

　　Tarjan算法是由Robert Tarjan（罗伯特·塔扬，不知有几位大神读对过这个名字） 发明的求有向图中强连通分量的算法。

　　预备知识：有向图，强连通。

　　有向图：由有向边的构成的图。需要注意的是这是Tarjan算法的前提和条件。

　　强连通：如果两个顶点可以相互通达，则称两个顶点 强连通(strongly connected)。如果有向图G的每两个顶点都 强连通，称G是一个强连通图。非 强连通图有向图的极大强连通子图，称为强连通分量(strongly connected components)。

　　For example:

　　

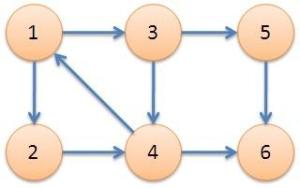
　　在这个有向图中1、2、3、4四个点可以互相到达，就称这四个点组成的子图为强连通分量。且这四个点两两强连通。

　　然后就可以开始学习神奇的Tarjan算法了！

　　Tarjan算法是用来求强连通分量的，它是一种基于DFS（深度优先搜索）的算法，每个强连通分量为搜索树中的一棵子树。并且运用了数据结构栈。

　　在介绍详细原理前，先引入两个非常重要的数组：dfn[ ] 与 low[ ]

　　dfn[ ]：就是一个时间戳（被搜到的次序），一旦某个点被DFS到后，这个时间戳就不再改变（且每个点只有唯一的时间戳）。所以常根据dfn的值来判断是否需要进行进一步的深搜。

　　low[ ]：该子树中，且仍在栈中的最小时间戳，像是确立了一个关系，low[ ]相等的点在同一强连通分量中。

　　注意初始化时 dfn[ ] = low[ ] = ++cnt.

　　

　　算法思路：

　　首先这个图不一定是一个连通图，所以跑Tarjan时要枚举每个点，若dfn[ ] == 0，进行深搜。

　　然后对于搜到的点寻找与其有边相连的点，判断这些点是否已经被搜索过，若没有，则进行搜索。若该点已经入栈，说明形成了环，则更新low.

　　在不断深搜的过程中如果没有路可走了（出边遍历完了），那么就进行回溯，回溯时不断比较low[ ]，去最小的low值。如果dfn[x]==low[x]则x可以看作是某一强连通分量子树的根，也说明找到了一个强连通分量，然后对栈进行弹出操作，直到x被弹出。

　　先来一波局部代码加深一下理解：

void tarjan(int now)
{
    dfn[now]=low[now]=++cnt;  //初始化
    stack[++t]=now;　　　　　　 //入栈操作
    v[now]=;　　　　　　　　    //v[]代表该点是否已入栈
    for(int i=f[now];i!=-;i=e[i].next)  //邻接表存图
        if(!dfn[e[i].v]) 　　　　　　　　　 //判断该点是否被搜索过
        {
            tarjan(e[i].v);
            low[now]=min(low[now],low[e[i].v]); //回溯时更新low[ ]，取最小值
        }
        else if(v[e[i].v])
            low[now]=min(low[now],dfn[e[i].v]); //一旦遇到已入栈的点，就将该点作为连通量的根
　　　　　　　　　　　　　　　　　　　　　　　　　　　　 //这里用dfn[e[i].v]更新的原因是：这个点可能
　　　　　　　　　　　　　　　　　　　　　　　　　　　　 //已经在另一个强连通分量中了但暂时尚未出栈，所
　　　　　　　　　　　　　　　　　　　　　　　　　　　　 //以now不一定能到达low[e[i].v]但一定能到达
　　　　　　　　　　　　　　　　　　　　　　　　　　　　 //dfn[e[i].v].
    if(dfn[now]==low[now])
    {
        int cur;
        do
        {
            cur=stack[t--];
            v[cur]=false;                       //不要忘记出栈
        }while(now!=cur);
    }
}

手动模拟一下过程：

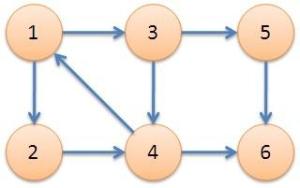
从1进入 dfn［1］＝ low［1］＝ ＋＋cnt = 1
入栈 1
由1进入2 dfn［2］＝low［2］＝ ＋＋cnt = 2
入栈 1 2
之后由2进入4 dfn［4］＝low［4］＝ ＋＋cnt = 3
入栈 1 2 4
之后由4进入 6 dfn［6］＝low［6］＝＋＋cnt = 4
入栈 1 2 4 6

6无出度，之后判断 dfn［6］＝＝low［6］
说明6是个强连通分量的根节点：6及6以后的点出栈并输出。

回溯到4后发现4找到了一个已经在栈中的点1，更新 low [ 4 ] = min ( low [ 4 ] , dfn [ 1 ] )

于是 low [ 4 ] = 1 .

由4继续回到2 Low[2] = min ( low [ 2 ] , low [ 4 ] ).
low［2］＝1；
由2继续回到1 判断 low[1] = min ( low [ 1 ] ,  low [ 2 ] ). 
low［1］还是 1
然后更新3的过程省略，大家可以自己手动模拟一下。

。。。。。。。。。

省略了1->3的更新过程之后，1的所有出边就跑完了

于是判断：low [ 1 ] == dfn [ 1 ] 说明以1为根节点的强连通分量已经找完了。

将栈中1以及1之后进栈的所有点，都出栈并输出。 

End

完整代码如下：

#include<iostream>  //输出所有强连通分量
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

int n,m,x,y,top=,cnt=,t,col;
int ans1=-,ans2=-,ans3=-;
int d[];
int a[];
int c[];
int f[];
int dfn[];
int low[];
int stack[];

bool v[];

struct edge{
    int u;
    int v;
    int w;
    int next;
}e[];

void Add(int u,int v,int w)
{
    ++top;
    e[top].u=u;
    e[top].v=v;
    e[top].w=w;
    e[top].next=f[u];
    f[u]=top;
}

int read()
{
    int x=;
    int k=;
    char c=getchar();
    while(c>''||c<'')
    {
        if(c=='-') k=-;
        c=getchar();
    }
    while(c>=''&&c<='')
        x=x*+c-'',
        c=getchar();
    return x*k;
}

void tarjan(int now)
{
    dfn[now]=low[now]=++cnt;
    stack[++t]=now;
    v[now]=;
    for(int i=f[now];i!=-;i=e[i].next)
        if(!dfn[e[i].v])
        {
            tarjan(e[i].v);
            low[now]=min(low[now],low[e[i].v]);
        }
        else if(v[e[i].v])
            low[now]=min(low[now],dfn[e[i].v]);
    int cur;
    if(dfn[now]==low[now])
    {
        do
        {
            cur=stack[t--];
            v[cur]=false;
            printf("%d ",cur);
        }while(now!=cur);
        printf("\n");
    }
}

int main()
{
    n=read();
    m=read();
    memset(f,-,sizeof f);
    for(int i=;i<=n;++i)
        a[i]=read();
    for(int i=;i<=m;++i)
    {
        x=read();
        y=read();
        Add(x,y,);
    }
    for(int i=;i<=n;++i)
        if(!dfn[i]) tarjan(i);
    return ;
}