uva10943(隔板法)
很裸的隔板法。
引用一下维基上对隔板法的解释:
现在有10个球,要放进3个盒子里
- ●●●●●●●●●●
隔2个板子,把10个球被隔开成3个部份
- ●|●|●●●●●●●●、●|●●|●●●●●●●、●|●●●|●●●●●●、●|●●●●|●●●●●、●|●●●●●|●●●●、●|●●●●●●|●●●、......
如此类推,10个球放进3个盒子的方法总数为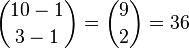
n个球放进k个盒子的方法总数为
问题等价于求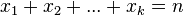 的可行解数,其中
的可行解数,其中 为正整数。
为正整数。
**如果允许有空盒子**:
现在有10个球,要放进3个盒子里,并允许空盒子。考虑10+3个球的情况:
- ●|●|●●●●●●●●●●●
从3个盒子里各拿走一个,得到一种情况,如此类推:
- ||●●●●●●●●●●、|●|●●●●●●●●●、|●●|●●●●●●●●、|●●●|●●●●●●●、|●●●●|●●●●●●、......
n个球放进k个盒子的方法总数(允许空盒子)为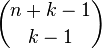 [2]
[2]
问题等价于求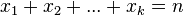 的可行解数,其中
的可行解数,其中 为非负整数。
为非负整数。
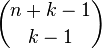 也是
也是 展开式的项数,这是因为展开后每一项肯定是a1^x1*a2^x2*......*ak^xk,而且x1+x2+...+xk=n.那就转化为上面那个问题了。
展开式的项数,这是因为展开后每一项肯定是a1^x1*a2^x2*......*ak^xk,而且x1+x2+...+xk=n.那就转化为上面那个问题了。
另一种变形:
减少球数用隔板法
将20个相同的小球放入编号分别为1,2,3,4的四个盒子中,要求每个盒子中的球数不少于它的编号数,求放法总数。
分析:先在编号1,2,3,4的四个盒子内分别放0,1,2,3个球,剩下14个无区别的球,问题等价于将14个球放入4个编号为1,2,3,4的四个盒子里,每个盒子至少有一个球的问题。
剩下14个无区别的球排成一列,共形成13个空,可以理解为有3块隔板,将排成一列的球隔成4段,每段至少1个,有C3/13=286(种)。
如果不用隔板法,亦可以递推来做:
按最后一个加上的数是几来分类,ans[n][k]=ans[n-1][k]+ans[n][k-1].其中ans[n][k-1]是最后一个加0,ans[n-1][k]是最后一位加的不是0.
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<algorithm>
#include<stack>
#include<queue>
using namespace std;
#define INF 1000000000
#define eps 1e-8
#define pii pair<int,int>
#define LL long long int
const int mod=1000000;
int n,k,ans,c[250][250];
int main()
{
//freopen("in6.txt","r",stdin);
//freopen("out.txt","w",stdout);
c[0][0]=1;
for(int i=1;i<=200;i++)
{
c[i][0]=c[i][i]=1;
for(int j=1;j<i;j++)
{
c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
}
}
while(scanf("%d%d",&n,&k)==2)
{
if(n==0&&k==0) break;
else
{
printf("%d\n",c[n+k-1][k-1]);
}
}
//fclose(stdin);
//fclose(stdout);
return 0;
}
uva10943(隔板法)的更多相关文章
- CF451E Devu and Flowers (隔板法 容斥原理 Lucas定理 求逆元)
Codeforces Round #258 (Div. 2) Devu and Flowers E. Devu and Flowers time limit per test 4 seconds me ...
- vijos1060 隔板法
排列组合问题 之前没有学过隔板法,随便学习了一下 其实挺好理解的 附上题解: 先只考虑一种球:因为有n个盒子每个盒子可以放任意多球,还可以空出来任意多球.所以可以考虑为n+1个盒子,最后一个盒子里面是 ...
- BZOJ 3028: 食物 [生成函数 隔板法 | 广义二项式定理]
3028: 食物 Time Limit: 3 Sec Memory Limit: 128 MBSubmit: 497 Solved: 331[Submit][Status][Discuss] De ...
- How do you add? UVA - 10943(组合数的隔板法!!)
题意: 把K个不超过N的非负整数加起来,使它们的和为N,有多少种方法? 隔板法...不会的可以买一本高中数学知识清单...给高中班主任打个广告.... 隔板法分两种...一种是不存在空集 = C(n- ...
- 51Nod 1509 加长棒(隔板法)
http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1509 思路: 直接去解可行的方法有点麻烦,所以应该用总的方法去减去不可行 ...
- hdu6397 Character Encoding 隔板法+容斥原理+线性逆元方程
题目传送门 题意:给出n,m,k,用m个0到n-1的数字凑出k,问方案数,mod一个值. 题目思路: 首先如果去掉数字范围的限制,那么就是隔板法,先复习一下隔板法. ①k个相同的小球放入m个不同的盒子 ...
- HDU4045 Machine scheduling —— 隔板法 + 第二类斯特林数
题目链接:https://vjudge.net/problem/HDU-4045 Machine scheduling Time Limit: 5000/2000 MS (Java/Others) ...
- 逆元 组合A(n,m) C(n,m)递推 隔板法
求逆元 https://blog.csdn.net/baidu_35643793/article/details/75268911 int inv[N]; void init(){ inv[] = ; ...
- light oj 1102 - Problem Makes Problem组合数学(隔板法)
1102 - Problem Makes Problem As I am fond of making easier problems, I discovered a problem. Actuall ...
随机推荐
- Django 进阶篇之 CSRF,COOIKE,SESSION
1.CSRF(Cross Site Request Forgery, 跨站域请求伪造) CSRF 背景与介绍 CSRF(Cross Site Request Forgery, 跨站域请求伪造)是一种网 ...
- Loadrunder之脚本篇——参数化在场景中的运用
Action() { lr_eval_string("{NewParam}"); lr_eval_string("{NewParam}"); return 0; ...
- LeetCode 14. Longest Common Prefix字典树 trie树 学习之 公共前缀字符串
所有字符串的公共前缀最长字符串 特点:(1)公共所有字符串前缀 (好像跟没说一样...) (2)在字典树中特点:任意从根节点触发遇见第一个分支为止的字符集合即为目标串 参考问题:https://lee ...
- yii框架的中的一些使用介绍
Yii框架的使用整理 获取配置文件中的数据 Yii::$app->params[‘配置文件中对应的参数名称’] 获取文件表单提交的数据 Yii::$app->request->pos ...
- Docker容器技术-基础命令
一.基础命令 1.运行一个镜像 [root@bogon ~]# docker run debian echo "Hello World" Unable to find image ...
- Shell编程之for和select循环
一.for和select循环 1.for循环语法 for 变量名 in 变量取值列表 do 指令... done C语言型for循环 for ((exp1; exp2; exp3)) do 指令... ...
- OC中NSSet去重细节
我们都知道,NSSet在存储数据时,不允许存储相同数据?那么,这里的相同该如何理解呢? 很多人都简单的理解为按照其存储对象的内存地址进行评判.其实不然.经过个人实验证明:当类型为NSString,NS ...
- git上面创建个人简历-链接
github创建个人在线简历: https://segmentfault.com/a/1190000006820290
- Go tail库
HP团队出的tail库,常用于日志收集 示例代码: package main import ( "github.com/hpcloud/tail" "fmt" ...
- hql学习记录
` String hql = "from SysUser o join o.set where owner_id = :newName"; Query query = this.g ...
