DS 图解归并排序

　　　　　　经典排序三剑客: 归并,堆排,快排。

　　　　　　今天,图解归并,一步步带你手撕代码~

　　　　　　归并排序,是采用"分而治之"思想的一个典型应用。

　　　　　　分治法精髓:

　　　　　　1.分 --- 将问题分解成若干个规模更小的问题

　　　　　　2.治 --- 将这些规模更小的问题逐个击破

　　　　　　3.合 --- 将已解决的子问题合并,最终得到"母"问题的解

　　　　　　知道了归并思想,如图,归并排序流程我们也能想到:

　　　　　　1.将待排序数组分解两个子序列,先让让左右两个子序列有序,然后再用两个有序数组合并的算法合并。那么怎么让左右子序列有序呢?

　　　　　　

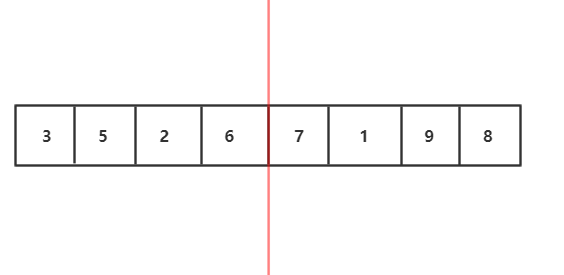
　　　　　　2.我们发现左右子序列还可以继续分解,左右子序列也可以通过自身的左右子序列排序后归并得到

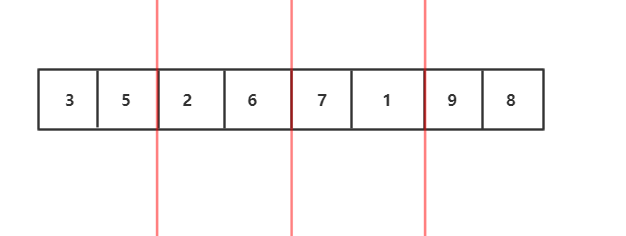
　　　　　　3.继续分解,分解到最小规模,也就是每个部分只有一个元素,我们发现每部分已经有序了

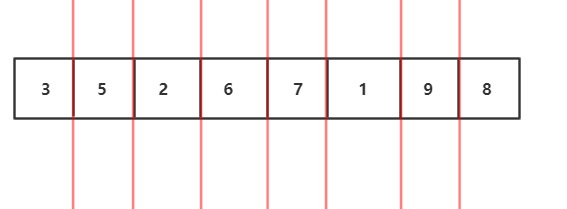
　　　　　　4.分治完,如图,开始用两个有序数组合并的算法合并,我们会发现这是一个递归过程,子问题的合并解就是该子问题"母问题"的解

　

　　

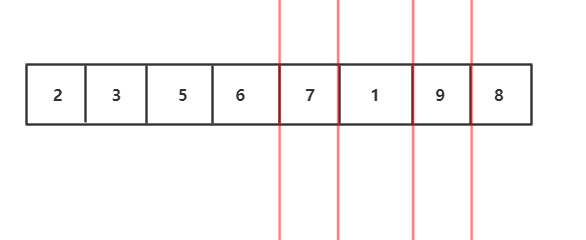
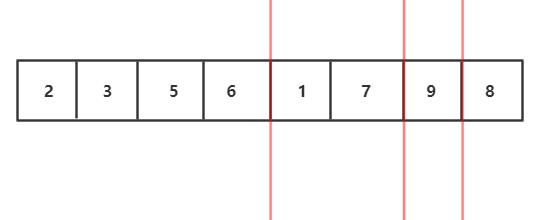
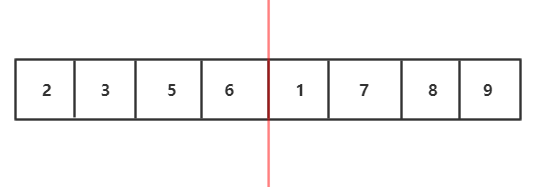
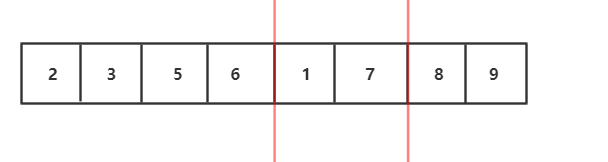
　　　　　　归并流程我们可以用递归实现,接下来要图解合并两个有序数组的算法 :

　　　　　　  

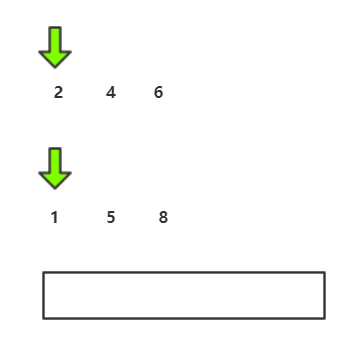
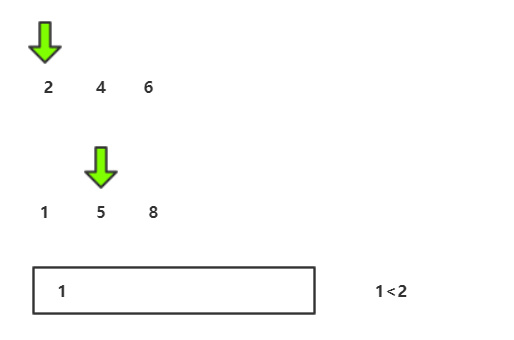
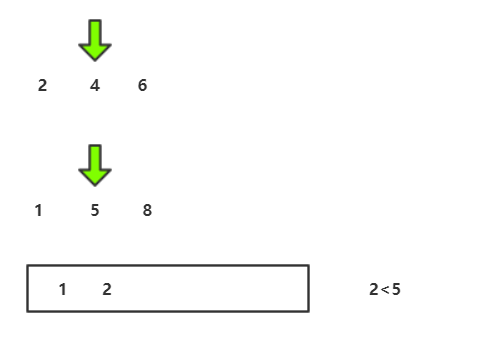
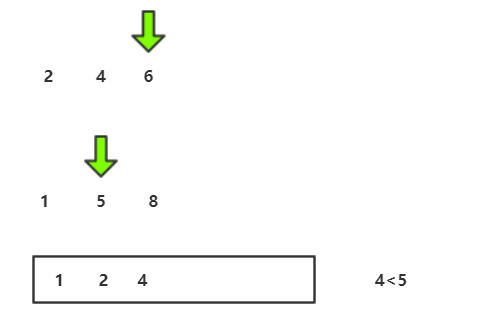
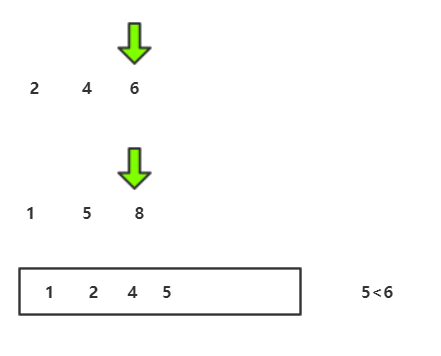
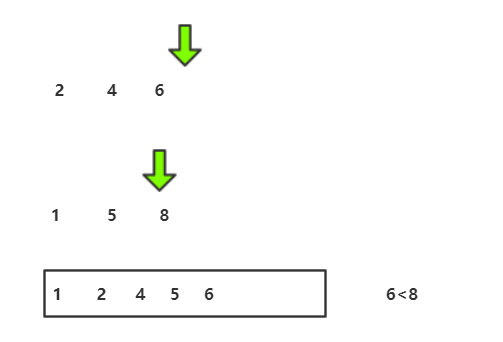
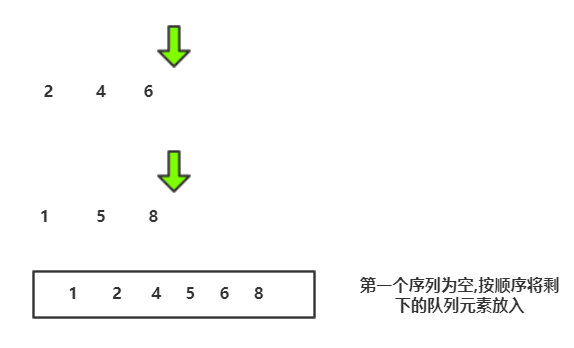
　　　　　　　　C代码实现:

#include<stdlib.h>
#include<stdio.h>

//归并两个有序数组
void  Merge(int* a, int left, int mid, int right,int* tmp)
{

    int begin1 = left, end1 = mid;
    int begin2 = mid+, end2 = right;
    int index = left;

    //比较排序(双指针)
    while (begin1<=end1 && begin2<=right)
    {
        if (a[begin1] <= a[begin2])
        {
            tmp[index++] = a[begin1++];
        }
        else
        {
            tmp[index++] = a[begin2++];
        }
    }
    //若剩余数组,按序插入
    while (begin1 <= end1)
        tmp[index++] = a[begin1++];

    while (begin2 <= end2)
        tmp[index++] = a[begin2++];
    //拷贝到原数组
    index = left;
    while (left <= right)
    {
        a[left++] = tmp[index++];
    }
}

//分解成最小子问题,回溯归并
void  Sort(int *a, int left, int right,int* tmp)
{
    //递归终止条件 : 只剩一个元素
    if (left >= right)
        return;

    int mid = left + (right-left)/;
    Sort(a, left, mid,tmp);
    Sort(a, mid+, right,tmp);
    Merge(a, left, mid, right,tmp);
}

//归并排序
void MergeSort(int *a, int n)
{
    int* tmp = (int *)malloc(sizeof(int)*n);
    Sort(a, , n - , tmp);
    free(tmp);
}

　时间复杂度：O(nlogn)

　　　 空间复杂度：O(N)，归并排序需要一个与原数组相同长度的数组做辅助来排序

稳定性: 稳定, 不管顺序如何,都要分解成最小子问题进行归并。