【leetcode-62，63，64 动态规划】 不同路径，最小路径和

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例:

输入:
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。

基础的动态规划问题，适合理解动态规范的想法

没有像之前设一个行和列+1的数组，这样更直观些不容易犯错

class Solution {
    public int minPathSum(int[][] grid) {
        int m = grid.length; //行数
        int n = grid[0].length; //列数
        int[][] dp = new int[m][n];
        //初始化第一行和第一列
        dp[0][0] = grid[0][0];
        for (int i=1;i<n;i++) {
            dp[0][i] = dp[0][i-1] + grid[0][i];
        }
        for (int i=1;i<m;i++) {
            dp[i][0] = dp[i-1][0] +grid[i][0];
        }
        for (int i=1;i<m;i++) {
            for (int j=1;j<n;j++) {
                dp[i][j] = grid[i][j] + Math.min(dp[i-1][j],dp[i][j-1]);
            }
        }

        return dp[m-1][n-1];
    }
}

【leetcode-62 动态规划】 不同路径

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

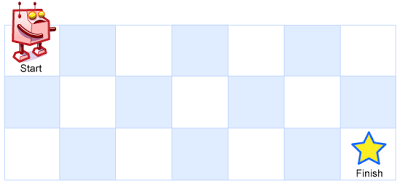
例如，上图是一个7 x 3 的网格。有多少可能的路径？

说明：m 和 n 的值均不超过 100。

示例 1:

输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右

示例 2:

输入: m = 7, n = 3
输出: 28

与上题类似，基础
我的：

class Solution {
    public int uniquePaths(int m,int n) {

        int[][] dp = new int[m][n];
        //初始化第一行和第一列
        dp[0][0] = 1;
        for (int i=1;i<n;i++) {
            dp[0][i] = 1;
        }
        for (int i=1;i<m;i++) {
            dp[i][0] = 1;
        }
        for (int i=1;i<m;i++) {
            for (int j=1;j<n;j++) {
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }

        return dp[m-1][n-1];
    }
}

63. 不同路径 II

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

说明：m 和 n 的值均不超过 100。

示例 1:

输入:
[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]
输出: 2
解释:
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int[][] dp = new int[m][n];
        //初始化第一行和第一列
        if (obstacleGrid[0][0] == 1) {
            dp[0][0] = 0;
        } else {
            dp[0][0] = 1;
        }
        for (int i=1;i<n;i++) {
            if (obstacleGrid[0][i] == 1)
                dp[0][i] = 0;
            else
            dp[0][i] = dp[0][i-1];
        }
        for (int i=1;i<m;i++) {
            if (obstacleGrid[i][0] == 1)
                dp[i][0] = 0;
            else
                dp[i][0] = dp[i-1][0];
        }
        for (int i=1;i<m;i++) {
            for (int j=1;j<n;j++) {
                if (obstacleGrid[i][j] == 1) {
                    dp[i][j] = 0;
                } else {
                    dp[i][j] = dp[i-1][j] + dp[i][j-1];
                }
            }
        }
        return dp[m-1][n-1];
    }