牛客CSP-S提高组赛前集训营2 T2沙漠点列

原题链接

算法不难，比赛的时候就和cyc大佬一起yy了正解，不过因为交的时候比较急（要回寝室惹），我有两数组开错大小直接爆到50，cyc大佬则只把文件输入关了一半，直接爆零(╯￣Д￣)╯┻━┻

要尽量使\(k\)次删边都能有贡献，那么很容易就想到割边。

所以我们先用\(\mathtt{tarjan}\)跑出所有割边，而每一条割边都能产生\(1\)的贡献，因此有\(sum_{bridge}\)条割边，就能增加\(sum_{bridge}\)个连通块。

若\(k \leqslant sum_{bridge}\)，那么最后的答案就是\(k + s\)（设原来的图有\(s\)个连通块）。

若\(k > sum_{bridge}\)，那么先删去这些割边，则剩下\(k' = k - sum_{bridge}\)条删边的次数。

然后我们考虑剩下的图该怎么去删边使贡献最大。

很容易发现删去割边后的图就是单个简单环或多个以点连接的简单环的集合。

对于多个以点连接的简单环，实际上我们可以把这多个连接的环拆成多个单环，如下图所示：



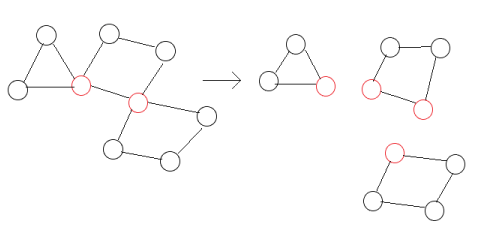
因为虽然将多个环拆开来会多出几个点，但是与此同时也增加了相同数目的连通块，因此对拆开后的多个单环进行删边的最大贡献是与原图相同的。

然后我们考虑怎么在这单环集合中删边使得贡献最大化，显然对于一个环，总是要删去一条没有贡献的边使其变为一条链，之后的每一次删边都能产生\(1\)的贡献。

所以我们需要尽量减少第一次删去无贡献边的次数，那么贪心策略就显而易见了，即将所有环按环的大小（即边数）降序排序，然后逐个尝试删边，直到删边次数\(k'\)用光或是边被删光为止。

对于单个环删边产生的贡献，若\(k' > size_{circle}\)（设环的大小为\(size_{circle}\)），则贡献为\(size_{circle} - 1\)；若\(k' <= size_{circle}\)，则贡献为\(k' - 1\)。

至于如何找出多个环（已经找出割边并标记），我们可以用\(\mathtt{dfs}\)，以时间戳标记的方式来找出，具体实现可以查看代码部分。

如果排序使用桶排，那么时间复杂度就是\(O(n + m)\)，像我这种懒的人直接用\(\mathtt{sort}\)就会多一个\(\log\)。

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e6 + 10;
const int M = 2e6 + 10;
int fi[N], di[M << 1], ne[M << 1], bridge[M << 1], dfn[N], low[N], circle[N], cir_s, l = 1, ti, bridge_sum;
//fi,di,ne为邻接表，bridge储存某一边是否是割边，dfn为时间戳，low为tarjan中的追溯值，circle储存每个单环的大小。
bool fa_l[M << 1];//dfs中用来判断边是否已经走过
inline int re()//快读
{
	int x = 0;
	char c = getchar();
	bool p = 0;
	for (; c < '0' || c > '9'; c = getchar())
		p |= c = '-';
	for (; c >= '0' && c <= '9'; c = getchar())
		x = x * 10 + c - '0';
	return p ? -x : x;
}
inline void add(int x, int y) { di[++l] = y; ne[l] = fi[x]; fi[x] = l; }//加边
inline int minn(int x, int y) { return x < y ? x : y; }
bool comp(int x, int y) { return x > y; }
void tarjan(int x, int la)//tarjan找割边模板
{
	int i, y;
	dfn[x] = low[x] = ++ti;
	for (i = fi[x]; i; i = ne[i])
		if (!dfn[y = di[i]])
		{
			tarjan(y, i);
			low[x] = minn(low[x], low[y]);
			if (low[y] > dfn[x])
				bridge[i] = bridge[i ^ 1] = 1, bridge_sum++;
		}
		else
			if (i ^ la ^ 1)
				low[x] = minn(low[x], dfn[y]);
}
void dfs(int x)//找出各个环
{
	int i, y;
	for (i = fi[x]; i; i = ne[i])
		if (!bridge[i] && !fa_l[i])//如果这条边不是割边且没有走过
			if (!dfn[y = di[i]])//如果边所连的点没有走过
				dfn[y] = dfn[x] + 1, fa_l[i] = fa_l[i ^ 1] = 1, dfs(y);//标记时间戳；记录这条边已走过；继续搜索
			else//如果走过了
				fa_l[i] = fa_l[i ^ 1] = 1, circle[++cir_s] = dfn[x] + 1 - dfn[y];//同样要记录这条边已走过，否则在回溯的时候会出锅；将该环的大小计入数组
}
int main()
{
	int i, n, m, k, x, y, ans = 0;
	n = re(); m = re(); k = re();
	for (i = 1; i <= m; i++)//输入图
	{
		x = re(); y = re();
		add(x, y); add(y, x);
	}
	for (i = 1; i <= n; i++)//tarjan找割边，同时统计原图连通块的个数
		if (!dfn[i])
			tarjan(i, 0), ans++;
	if (k <= bridge_sum)//若k不够删去所有割边，就直接输出答案
		return printf("%d", k + ans), 0;
	ans += bridge_sum; k -= bridge_sum;//统计答案并将k减去割边数
	memset(dfn, 0, sizeof(dfn));
	for (i = 1; i <= n; i++)//找环
		if (!dfn[i])
			dfn[i] = 1, dfs(i);
	sort(circle + 1, circle + cir_s + 1, comp);
	for (i = 1; i <= cir_s; i++)//贪心删边并统计贡献
		if (k >= circle[i])
			ans += circle[i] - 1, k -= circle[i];
		else
		{
			ans += k - 1;
			break;
		}
	return printf("%d", ans), 0;
}