<转>Logistic回归总结

转自http://blog.csdn.net/dongtingzhizi/article/details/15962797

当我第一遍看完台大的机器学习的视频的时候，我以为我理解了逻辑回归，可后来越看越迷糊，直到看到了这篇文章，豁然开朗

基本原理

Logistic Regression和Linear Regression的原理是相似的，按照我自己的理解，可以简单的描述为这样的过程：

（1）找一个合适的预测函数（Andrew Ng的公开课中称为hypothesis），一般表示为h函数，该函数就是我们需要找的分类函数，它用来预测输入数据的判断结果。这个过程时非常关键的，需要对数据有一定的了解或分析，知道或者猜测预测函数的“大概”形式，比如是线性函数还是非线性函数。

（2）构造一个Cost函数（损失函数），该函数表示预测的输出（h）与训练数据类别（y）之间的偏差，可以是二者之间的差（h-y）或者是其他的形式。综合考虑所有训练数据的“损失”，将Cost求和或者求平均，记为J(θ)函数，表示所有训练数据预测值与实际类别的偏差。

（3）显然，J(θ)函数的值越小表示预测函数越准确（即h函数越准确），所以这一步需要做的是找到J(θ)函数的最小值。找函数的最小值有不同的方法，Logistic Regression实现时有的是梯度下降法（Gradient Descent）。

具体过程

(1)  构造预测函数

Logistic Regression虽然名字里带“回归”，但是它实际上是一种分类方法，用于两分类问题（即输出只有两种）。根据第二章中的步骤，需要先找到一个预测函数（h），显然，该函数的输出必须是两个值（分别代表两个类别），所以利用了Logistic函数（或称为Sigmoid函数），函数形式为：

对应的函数图像是一个取值在0和1之间的S型曲线（图1）。

图1

接下来需要确定数据划分的边界类型，对于图2和图3中的两种数据分布，显然图2需要一个线性的边界，而图3需要一个非线性的边界。接下来我们只讨论线性边界的情况。

图2

图3

对于线性边界的情况，边界形式如下：

构造预测函数为：

hθ(x)函数的值有特殊的含义，它表示结果取1的概率，因此对于输入x分类结果为类别1和类别0的概率分别为：

(2)构造Cost函数

Andrew Ng在课程中直接给出了Cost函数及J(θ)函数如式（5）和（6），但是并没有给出具体的解释，只是说明了这个函数来衡量h函数预测的好坏是合理的。

实际上这里的Cost函数和J(θ)函数是基于最大似然估计推导得到的。下面详细说明推导的过程。（4）式综合起来可以写成：

取似然函数为：

对数似然函数为：

最大似然估计就是要求得使l(θ)取最大值时的θ，其实这里可以使用梯度上升法求解，求得的θ就是要求的最佳参数。但是，在Andrew
Ng的课程中将J(θ)取为（6）式，即：

因为乘了一个负的系数-1/m，所以J(θ)取最小值时的θ为要求的最佳参数。

(3)梯度下降法求J(θ)的最小值

求J(θ)的最小值可以使用梯度下降法，根据梯度下降法可得θ的更新过程：

式中为α学习步长，下面来求偏导：

上式求解过程中用到如下的公式：

因此，（11）式的更新过程可以写成：

因为式中α本来为一常量，所以1/m一般将省略，所以最终的θ更新过程为：

之后，参数更新为：

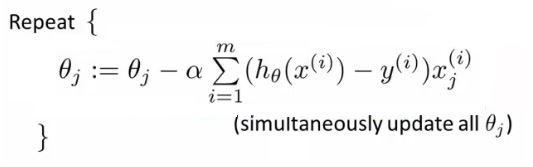
终止条件：

目前指定迭代次数。后续会谈到更多判断收敛和确定迭代终点的方法。

---

另外，补充一下，3.2节中提到求得l(θ)取最大值时的θ也是一样的，用梯度上升法求（9）式的最大值，可得：

观察上式发现跟（14）是一样的，所以，采用梯度上升发和梯度下降法是完全一样的，这也是《机器学习实战》中采用梯度上升法的原因。